题目内容
长方形的周长为24cm,其中一边为xcm(其中x>0),面积为ycm2,则这样的长方形中y与x的关系可以写为( )
A. y=x2 B. y=12﹣x2 C. y=(12﹣x)•x D. y=2(12﹣x)
C 【解析】∵长方形的周长为24cm,其中一边为x(其中x>0), ∴长方形的另一边长为12-x, ∴y=(12-x)•x. 故选C.
练习册系列答案
相关题目
下表是佳佳往表妹家打长途电话的收费记录:
时间/min | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
电话费/元 | 0.6 | 1.2 | 1.8 | 2.4 | 3.0 | 3.6 | 4.2 |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)若佳佳的通话时间是10 min,则需要付多少电话费?
(1)反映了电话费与通话时间之间的关系;其中通话时间是自变量,电话费是因变量. (2)需付6元电话费. 【解析】分析:(1)根据函数的定义可知,通话时间是自变量,电话费是因变量; (2)观察图表中的数据,1分钟0.6,两分钟1.2,相差0.6,可知成等差数列,从而求解. 本题解析: (1)通话时间与电话费;其中通话时间是自变量,电话费是因变量; (2)设时间为x...

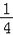 d2=0有两个相等的实数根,其中R、r分别是⊙O1、⊙O2的半径,d为两圆的圆心距,则⊙O1与⊙O2的位置关系是( )
d2=0有两个相等的实数根,其中R、r分别是⊙O1、⊙O2的半径,d为两圆的圆心距,则⊙O1与⊙O2的位置关系是( )

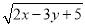 +(2x+3y-13)2=0,则2x-y的值为________.
+(2x+3y-13)2=0,则2x-y的值为________.