Question

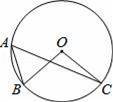
如图，在△ABC中，∠B=60°，⊙O是△ABC外接圆，过点A作⊙O的切线，交CO的延长线于P点，CP交⊙O于D；

（1）求证：AP=AC；

（2）若AC=3，求PC的长．

Answer 1

【考点】切线的性质；圆周角定理；解直角三角形．

【专题】几何综合题．

【分析】（1）连接OA，可得∠AOC=120°，所以，可得∠P=∠C=30°，即可证明；

（2）AC=3，所以，PO=，所以PC=3．

【解答】（1）证明：连接AO，则AO⊥PA，∠AOC=2∠B=120°，

∴∠AOP=60°，

∴∠P=30°，

又∵OA=OC，

∴∠ACP=30°，

∴∠P=∠ACP，

∴AP=AC．

（2）解：在Rt△PAO中，∠P=30°，PA=3，

∴AO=，

∴PO=2；

∵CO=OA=，

∴PC=PO+OC=3．

【点评】本题主要考查了直角三角形、圆周角及切线的性质定理，综合性比较强，熟记定理及性质，才是解答的关键．