题目内容
如图，在Rt△ABC中，∠ACB=90°，D是AB的中点，过D点作AB的垂线交AC于点E，BC=6，sinA=
| 3 |
| 5 |
A、
| ||
| B、4 | ||
| C、5 | ||
D、
|
考点：相似三角形的判定与性质,勾股定理,锐角三角函数的定义
专题：
分析：由BC=6，sinA=
，可求得AB=10，则BD=AD=5，由条件可知△ADE∽△ACB，可得
=
，代入可求得AE．
| 3 |
| 5 |
| AE |
| AB |
| AD |
| AC |
解答：解：∵Rt△ABC中，∠ACB=90°，
∴sinA=
=
，且BC=6，
∴AB=10，由勾股定理可求得AC=8，
又∵D为AB中点，
∴BD=AD=5，
在△ADE和△ACB中，
∵∠ADE=∠ACB，∠DAE=∠CAB，
∴△ADE∽△ACB，
∴
=
，
∴
=
，
∴AE=
，
故选A．
∴sinA=
| BC |
| AB |
| 3 |
| 5 |
∴AB=10，由勾股定理可求得AC=8，
又∵D为AB中点，
∴BD=AD=5，
在△ADE和△ACB中，
∵∠ADE=∠ACB，∠DAE=∠CAB，
∴△ADE∽△ACB，
∴
| AE |
| AB |
| AD |
| AC |
∴
| AE |
| 10 |
| 5 |
| 8 |
∴AE=
| 25 |
| 4 |
故选A．
点评：本题主要考查相似三角形的判定和性质和三角函数的定义，掌握三角函数的定义是解题的关键．
练习册系列答案
相关题目
有下列四个命题：
①对顶角相等；
②内错角相等；
③有两边和其中一边的对角对应相等的两个三角形全等；
④在同一平面内，如果两条直线都垂直于第三条直线，那么这两条直线平行．
其中真命题有（ ）
①对顶角相等；
②内错角相等；
③有两边和其中一边的对角对应相等的两个三角形全等；
④在同一平面内，如果两条直线都垂直于第三条直线，那么这两条直线平行．
其中真命题有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
如图，P为△ABC的边AB、AC的垂直平分线的交点，∠BAC=50°，求∠BPC的度数．
如图，半圆O的直径AB=10cm，弦AD=3| 10 |
A、4
| ||
| B、8cm | ||
C、2
| ||
| D、6cm |
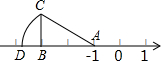如图，直角三角形ABC的直角边AB在数轴上，点A表示的实数为-1，以A为圆心，AC的长为半径作弧交数轴的负半轴于D，若CB=1，AB=2，则点D表示的实数为（ ）A、
| ||
B、-
| ||
C、-
| ||
D、-
|