题目内容
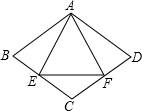如图，等边三角形AEF与菱形ABCD有一公共顶点A，E、F在BC、CD上，且它们的边长相等，则∠B=________度．
80
分析：正△AEF的边长与菱形ABCD的边长相等，所以AB=AE，AF=AD，根据邻角之和为180°即可求得∠B的度数．
解答：正△AEF的边长与菱形ABCD的边长相等，所以AB=AE，AF=AD，
设∠B=x，则∠BAD=180°-x，
∠BAE=∠DAF=180°-2x，
又∵∠BAE+∠EAF+∠FAD=∠BAD
即180°-2x+180°-2x+60°=180°-x
解得x=80°，
故答案为：80°．
点评：本题考查了正三角形各内角为60°、各边长相等的性质，考查了菱形邻角之和为180°的性质，本题中根据关于x的等量关系式求x的值是解题的关键．
分析：正△AEF的边长与菱形ABCD的边长相等，所以AB=AE，AF=AD，根据邻角之和为180°即可求得∠B的度数．
解答：正△AEF的边长与菱形ABCD的边长相等，所以AB=AE，AF=AD，
设∠B=x，则∠BAD=180°-x，
∠BAE=∠DAF=180°-2x，
又∵∠BAE+∠EAF+∠FAD=∠BAD
即180°-2x+180°-2x+60°=180°-x
解得x=80°，
故答案为：80°．
点评：本题考查了正三角形各内角为60°、各边长相等的性质，考查了菱形邻角之和为180°的性质，本题中根据关于x的等量关系式求x的值是解题的关键．
练习册系列答案
相关题目
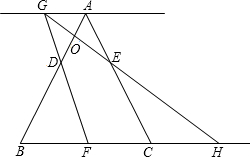运动的时间为t秒．当t＞0时，直线FD与过点A且平行于BC的直线相交于点G，GE的延长线与BC的延长线相交于点H，AB与GH相交于点O．
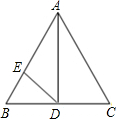如图，等边三角形ABC中，D、E在BC、AB上，且BD=DC，AE=2BE，则tan∠ADE=
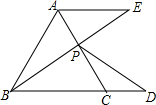（2012•南京二模）如图，等边三角形ABC的边长为5，点P在边AC上，且AP=2，点D在直线BC上，且PD=PB，作AE∥BC，交BP于点E．请你求出
如图，等边三角形ABC中，D、E分别为AB、BC边上的两个动点，且总使AD=BE，AE与CD交于点F，AG⊥CD于点G，则∠FAG=