Question

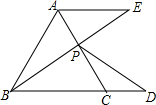（2012•南京二模）如图，等边三角形ABC的边长为5，点P在边AC上，且AP=2，点D在直线BC上，且PD=PB，作AE∥BC，交BP于点E．请你求出

AE

CD

的值．

Answer 1

分析：利用等边三角形的性质和AD∥BC，首先证明∠PCD=∠BAE，再利用已知条件证明∠E=∠D，进而证明△BEA∽△PDC，由相似三角形的性质得到关于

AE

CD

的关系式，再代入数据计算即可．

解答：解：∵等边三角形ABC，
∴∠ABC=∠ACB=60°．
∵AE∥BC，
∴∠BAE=120°，
∵∠ACB=60°，
∴∠PCD=120°．
∴∠PCD=∠BAE．
∵PB=PD，
∴∠PBD=∠D． 
∵AE∥BC，
∴∠E=∠EBD．
∴△BEA∽△PDC．
∴

AB

CP

=

AE

CD

．
∵AC=5，AP=2，
∴CP=3．
又∵AB=5，
∴

AE

CD

=

AB

CP

=

5

3

．

点评：本题考查了等边三角形的性质、平行线的性质、相似三角形的判定和性质，解题的关键是利用有两对角相等的三角形相似证明△BEA∽△PDC．