题目内容
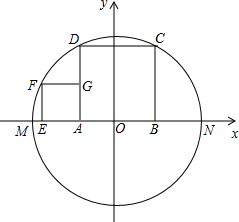 如图,正方形ABCD与正方形AEFG的顶点E、A、B在同一直线上,以AB所在直线为x轴、AB中点O为原点建立平面直角坐标系,以O为圆心的⊙O恰好经过C、D、F三点,交x轴于点M、N,已知正方形ABCD的边长为4.
如图,正方形ABCD与正方形AEFG的顶点E、A、B在同一直线上,以AB所在直线为x轴、AB中点O为原点建立平面直角坐标系,以O为圆心的⊙O恰好经过C、D、F三点,交x轴于点M、N,已知正方形ABCD的边长为4.(1)求正方形AEFG的边长,并直接写出点C、F的坐标;
(2)抛物线y=ax2+bx经过C、F两点,求抛物线的解析式;
(3)在(2)中的抛物线上是否存在点H,使得以M、N、H为顶点的三角形为直角三角形?若存在,请直接写出所有满足条件的点H坐标;若不存在,请说明理由.
考点:圆的综合题
专题:
分析:(1)设正方形AEFG的边长为λ,运用勾股定理列出关于λ的方程,求出λ,问题即可解决.
(2)将C、F两点的坐标代入抛物线解析式,列出关于a、b的方程组,求出a、b的值,问题即可解决.
(3)运用分类讨论的数学思想,当MN为直角三角形的直角边或斜边时,借助抛物线解析式、勾股定理等知识逐一讨论解析,问题即可解决.
(2)将C、F两点的坐标代入抛物线解析式,列出关于a、b的方程组,求出a、b的值,问题即可解决.
(3)运用分类讨论的数学思想,当MN为直角三角形的直角边或斜边时,借助抛物线解析式、勾股定理等知识逐一讨论解析,问题即可解决.
解答: 解:(1)如图,连接OC、OF;
解:(1)如图,连接OC、OF;
设正方形AEFG的边长为λ;由题意得:
∠FEO=∠OBC=90°,OE=2+λ,OC=OF;OB=2,BC=4;
由勾股定理得:OC2=OB2+BC2,OF2=OE2+EF2,
∴22+42=(2+λ)2+λ2,
解得:λ=2或-4(舍去).
∴正方形AEFG的边长为2,点C、F的坐标分别为C(2,4)、F(-4,2).
(2)∵抛物线y=ax2+bx经过C、F两点,
∴
,
解得:a=
,b=
,
∴抛物线的解析式为y=
x2+
x.
(3)存在.
满足条件的点H的坐标为:(-2
,
)、(2
,
).
 解:(1)如图,连接OC、OF;
解:(1)如图,连接OC、OF;设正方形AEFG的边长为λ;由题意得:
∠FEO=∠OBC=90°,OE=2+λ,OC=OF;OB=2,BC=4;
由勾股定理得:OC2=OB2+BC2,OF2=OE2+EF2,
∴22+42=(2+λ)2+λ2,
解得:λ=2或-4(舍去).
∴正方形AEFG的边长为2,点C、F的坐标分别为C(2,4)、F(-4,2).
(2)∵抛物线y=ax2+bx经过C、F两点,
∴
|
解得:a=
| 5 |
| 12 |
| 7 |
| 6 |
∴抛物线的解析式为y=
| 5 |
| 12 |
| 7 |
| 6 |
(3)存在.
满足条件的点H的坐标为:(-2
| 5 |
25-7
| ||
| 3 |
| 5 |
25+7
| ||
| 3 |
点评:该题是以平面直角坐标系和圆为载体,以考查点的坐标的定义、勾股定理、待定系数法等几何知识点为核心构造而成的一道坐标型几何题;对综合的分析问题解决问题的能力、求解运算能力等均提出了较高的要求.

练习册系列答案
相关题目
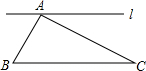 如图,已知∠A=90°,∠C=30°,AB=2,过点A的直线l与BC平行.若D是l上的一点,且BD=DC,求AD两点间的距离.
如图,已知∠A=90°,∠C=30°,AB=2,过点A的直线l与BC平行.若D是l上的一点,且BD=DC,求AD两点间的距离.