题目内容
10.已知抛物线y=(x-1)2-4,指出其对称轴,顶点坐标及图象与x轴、y轴的交点坐标.分析 根据y=(x-h)2+k的对称轴是x=h,顶点坐标(h,k),x=0时,可得图象与y轴的交点,y=0时,可得图象与x轴的交点.
解答 解:y=(x-1)2-4,指出其对称轴x=1,
顶点坐标(1,-4);
图象与x轴的交点坐标(3,0)或(-1,0),
图象与y轴的交点坐标(0,-3).
点评 本体考察了二次函数的图象与性质,y=(x-h)2+k的对称轴是x=h,顶点坐标(h,k).

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
9.阅读下列材料:如果(x+1)2-9=0,那么(x+1)2-32=(x+1+3)(x+1-3)=(x+4)(x-2),则(x+4)(x-2)=0,由此可知:x1=-4,x2=2.根据以上材料计算x2-2x-1=0的根为( )
| A. | x1=1+$\sqrt{2}$,x2=1-$\sqrt{2}$ | B. | x1=-1+$\sqrt{2}$,x2=11-$\sqrt{2}$ | C. | x1=-1+$\sqrt{2}$,x2=1-$\sqrt{2}$ | D. | x1=1+$\sqrt{2}$,x2=-1-$\sqrt{2}$ |
 如图,点D,E分别是ABC的边BC,AC上的点,BE,AD交于F,已知AB=AC,∠BAC=∠AFE=2∠ACB=2α,G为AC上的点,∠AEB=∠CGD.探究线段AE,GC的数量关系,并说明理由.
如图,点D,E分别是ABC的边BC,AC上的点,BE,AD交于F,已知AB=AC,∠BAC=∠AFE=2∠ACB=2α,G为AC上的点,∠AEB=∠CGD.探究线段AE,GC的数量关系,并说明理由.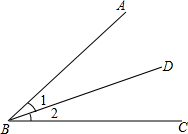 如图,
如图,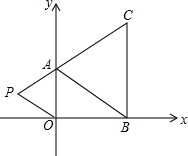 如图,在直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式,|a+b-5|+$\sqrt{2a-b-1}$=0,(c-4)2≤0.
如图,在直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式,|a+b-5|+$\sqrt{2a-b-1}$=0,(c-4)2≤0.