题目内容
我县某工艺厂为配合60年国庆,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
(1)把上表中 、
、 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想 与
与 的函数关系,并求出函数关系式;
的函数关系,并求出函数关系式;

(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)我县物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
销售单价 (元∕件) (元∕件) | …… | 30 | 40 | 50 | 60 | …… |
每天销售量 (件) (件) | …… | 500 | 400 | 300 | 200 | …… |
(1)把上表中
 、
、 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想 与
与 的函数关系,并求出函数关系式;
的函数关系,并求出函数关系式; 
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)我县物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
(1) =-10
=-10 +800(2)当销售单价定为50元∕件时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元(3)45元
+800(2)当销售单价定为50元∕件时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元(3)45元
 =-10
=-10 +800(2)当销售单价定为50元∕件时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元(3)45元
+800(2)当销售单价定为50元∕件时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元(3)45元解:(1)画图如图; 1分
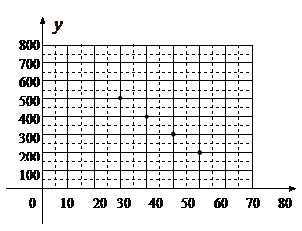
由图可猜想 与
与 是一次函数关系,····· 3分
是一次函数关系,····· 3分
设这个一次函数为 =
= 
 +
+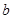 (k≠0)
(k≠0)
∵这个一次函数的图象经过(30,500)
(40,400)这两点,
∴ 解得
解得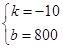 ……5分
……5分
∴函数关系式是: =-10
=-10 +800 ……6分
+800 ……6分
(2)设工艺厂试销该工艺品每天获得的利润是W元,依题意得
W=( -20)(-10
-20)(-10 +800)······················· 8分
+800)······················· 8分
=-10
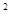 +1000
+1000 -16000
-16000
=-10( -50)
-50)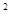 +9000 ························ 9分
+9000 ························ 9分
∴当 =50时,W有最大值9000.
=50时,W有最大值9000.
所以,当销售单价定为50元∕件时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元. 10分
(3)对于函数 W=-10( -50)
-50)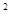 +9000,当
+9000,当 ≤45时,
≤45时,
W的值随着 值的增大而增大, ······················· 11分
值的增大而增大, ······················· 11分
∴销售单价定为45元∕件时,工艺厂试销该工艺品每天获得的利润最大.····· 12分
(1)用待定系数法(将两个点待入一次函数解析式即可)
(2)根据利润=销售总价-成本总价,得出利润与销售单价的关系即可
(3)由(2)知利润W与销售单价x的关系:W=-10( -50)
-50)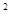 +9000,销售单价最高不能超过45元/件,W随x的增大而减小,故销售单价定为45元∕件时,工艺厂试销该工艺品每天获得的利润最大
+9000,销售单价最高不能超过45元/件,W随x的增大而减小,故销售单价定为45元∕件时,工艺厂试销该工艺品每天获得的利润最大
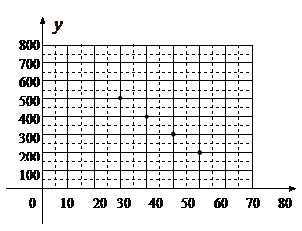
由图可猜想
 与
与 是一次函数关系,····· 3分
是一次函数关系,····· 3分设这个一次函数为
 =
= 
 +
+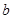 (k≠0)
(k≠0)∵这个一次函数的图象经过(30,500)
(40,400)这两点,
∴
 解得
解得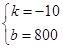 ……5分
……5分 ∴函数关系式是:
 =-10
=-10 +800 ……6分
+800 ……6分(2)设工艺厂试销该工艺品每天获得的利润是W元,依题意得
W=(
 -20)(-10
-20)(-10 +800)······················· 8分
+800)······················· 8分=-10

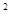 +1000
+1000 -16000
-16000=-10(
 -50)
-50)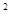 +9000 ························ 9分
+9000 ························ 9分∴当
 =50时,W有最大值9000.
=50时,W有最大值9000.所以,当销售单价定为50元∕件时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元. 10分
(3)对于函数 W=-10(
 -50)
-50)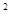 +9000,当
+9000,当 ≤45时,
≤45时,W的值随着
 值的增大而增大, ······················· 11分
值的增大而增大, ······················· 11分∴销售单价定为45元∕件时,工艺厂试销该工艺品每天获得的利润最大.····· 12分
(1)用待定系数法(将两个点待入一次函数解析式即可)
(2)根据利润=销售总价-成本总价,得出利润与销售单价的关系即可
(3)由(2)知利润W与销售单价x的关系:W=-10(
 -50)
-50) +9000,销售单价最高不能超过45元/件,W随x的增大而减小,故销售单价定为45元∕件时,工艺厂试销该工艺品每天获得的利润最大
+9000,销售单价最高不能超过45元/件,W随x的增大而减小,故销售单价定为45元∕件时,工艺厂试销该工艺品每天获得的利润最大
练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 ⑤a+b+c>m(am+b)+c,(m>1的实数),其中正确的结论有( )
⑤a+b+c>m(am+b)+c,(m>1的实数),其中正确的结论有( )
 的图像可能是 【 】
的图像可能是 【 】

 的顶点坐标是( )
的顶点坐标是( )



