题目内容
已知等腰三角形ABC的两个顶点分别是A(0,1)、B(0,3),第三个顶点C在x轴的正半轴上.关于y轴对称的抛物线y=ax2+bx+c经过A、D(3,-2)、P三点,且点P关于直线AC的对称点在x轴上.
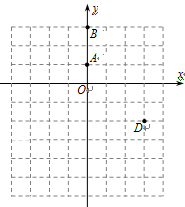
(1)求直线BC的解析式;
(2)求抛物线y=ax2+bx+c的解析式及点P的坐标;
(3)设M是y轴上的一个动点,求PM+CM的取值范围.

(1)求直线BC的解析式;
(2)求抛物线y=ax2+bx+c的解析式及点P的坐标;
(3)设M是y轴上的一个动点,求PM+CM的取值范围.
(1) (2)
(2) ,
, ,
, .(3),当点
.(3),当点 的坐标是
的坐标是 时,
时,
 ,当点
,当点 的坐标是
的坐标是 时,
时, 

 (2)
(2) ,
, ,
, .(3),当点
.(3),当点 的坐标是
的坐标是 时,
时,
 ,当点
,当点 的坐标是
的坐标是 时,
时, 

解:(1) ,
, ,
,
 ,
,

 是等腰三角形,且点
是等腰三角形,且点 在
在 轴的正半轴上,
轴的正半轴上,
 ,
,

 .
.
 .
.
设直线 的解析式为
的解析式为 ,
,
 ,
, .
.
 直线
直线 的解析式为
的解析式为 .····················· 4分
.····················· 4分
(2) 抛物线
抛物线 关于
关于 轴对称,
轴对称, .············ 5分
.············ 5分

又抛物线 经过
经过 ,
, 两点.
两点.

 解得
解得
 抛物线的解析式是
抛物线的解析式是 .······· 7分
.······· 7分
在 中,
中, ,易得
,易得 .
.
在 中,
中, ,
, ,易得
,易得 .
.

 是
是 的角平分线.
的角平分线.
 直线
直线 与
与 轴关于直线
轴关于直线 对称.
对称.
点 关于直线
关于直线 的对称点在
的对称点在 轴上,则符合条件的点
轴上,则符合条件的点 就是直线
就是直线 与抛物线
与抛物线 的交点. 8分
的交点. 8分
 点
点 在直线
在直线 :
: 上,
上,
故设点 的坐标是
的坐标是 .
.
又点
 在抛物线
在抛物线 上,
上,

 .解得
.解得 ,
, .
.
故所求的点 的坐标是
的坐标是 ,
, .··············· 10分
.··············· 10分
(3)要求 的取值范围,可先求
的取值范围,可先求 的最小值.
的最小值.
I)当点 的坐标是
的坐标是 时,点
时,点 与点
与点 重合,故
重合,故 .
.
显然 的最小值就是点
的最小值就是点 到
到 轴的距离为
轴的距离为 ,
,
 点
点 是
是 轴上的动点,
轴上的动点,
 无最大值,
无最大值,

 .···· 13分
.···· 13分
II)当点 的坐标是
的坐标是 时,由点
时,由点 关于
关于 轴的对称点
轴的对称点 ,故只要求
,故只要求 的最小值,显然线段
的最小值,显然线段 最短.易求得
最短.易求得 .
.

 的最小值是6.
的最小值是6.
同理 没有最大值,
没有最大值,
 的取值范围是
的取值范围是
 .
.
综上所述,当点 的坐标是
的坐标是 时,
时,
 ,
,
当点 的坐标是
的坐标是 时,
时, 
 .··············· 15分
.··············· 15分
(1)设直线解析式为 ,用待定系数法,由勾股定理得到点
,用待定系数法,由勾股定理得到点 ,而
,而 ,把它们代入即可
,把它们代入即可
(2)关于 对称,则对称轴
对称,则对称轴 ,再把点
,再把点 的坐标代入
的坐标代入 即可;由于点P关于直线AC的对称点在x轴上,利用直角三角形三角函数,得出直线
即可;由于点P关于直线AC的对称点在x轴上,利用直角三角形三角函数,得出直线 与
与 轴关于直线
轴关于直线 对称,则符合条件的点
对称,则符合条件的点 就是直线
就是直线 与抛物线
与抛物线 的交点,把
的交点,把 与
与 组成方程组,求方程组的解即可
组成方程组,求方程组的解即可
(3)要求范围,要求边界值,即求PM+CM的最小值和最大值,当点 的坐标是
的坐标是 时,则
时,则 ,故最小值为
,故最小值为 ,但没有最大值,故
,但没有最大值,故
 ;当
;当
点 的坐标是
的坐标是 时,把点
时,把点 和点
和点 分到
分到 轴的两侧,两点间连线最短,连线与
轴的两侧,两点间连线最短,连线与 轴的交点就点
轴的交点就点 ,
, 的最小值是
的最小值是 ,同样没有最大值,故
,同样没有最大值,故

 ,
, ,
,
 ,
,
 是等腰三角形,且点
是等腰三角形,且点 在
在 轴的正半轴上,
轴的正半轴上,
 ,
,
 .
.
 .
.设直线
 的解析式为
的解析式为 ,
,
 ,
, .
. 直线
直线 的解析式为
的解析式为 .····················· 4分
.····················· 4分(2)
 抛物线
抛物线 关于
关于 轴对称,
轴对称, .············ 5分
.············ 5分
又抛物线
 经过
经过 ,
, 两点.
两点.
 解得
解得
 抛物线的解析式是
抛物线的解析式是 .······· 7分
.······· 7分在
 中,
中, ,易得
,易得 .
.在
 中,
中, ,
, ,易得
,易得 .
.
 是
是 的角平分线.
的角平分线. 直线
直线 与
与 轴关于直线
轴关于直线 对称.
对称.点
 关于直线
关于直线 的对称点在
的对称点在 轴上,则符合条件的点
轴上,则符合条件的点 就是直线
就是直线 与抛物线
与抛物线 的交点. 8分
的交点. 8分 点
点 在直线
在直线 :
: 上,
上,故设点
 的坐标是
的坐标是 .
.又点

 在抛物线
在抛物线 上,
上,
 .解得
.解得 ,
, .
.故所求的点
 的坐标是
的坐标是 ,
, .··············· 10分
.··············· 10分(3)要求
 的取值范围,可先求
的取值范围,可先求 的最小值.
的最小值.I)当点
 的坐标是
的坐标是 时,点
时,点 与点
与点 重合,故
重合,故 .
.显然
 的最小值就是点
的最小值就是点 到
到 轴的距离为
轴的距离为 ,
, 点
点 是
是 轴上的动点,
轴上的动点,
 无最大值,
无最大值,

 .···· 13分
.···· 13分II)当点
 的坐标是
的坐标是 时,由点
时,由点 关于
关于 轴的对称点
轴的对称点 ,故只要求
,故只要求 的最小值,显然线段
的最小值,显然线段 最短.易求得
最短.易求得 .
.
 的最小值是6.
的最小值是6.同理
 没有最大值,
没有最大值,
 的取值范围是
的取值范围是
 .
.综上所述,当点
 的坐标是
的坐标是 时,
时,
 ,
,当点
 的坐标是
的坐标是 时,
时, 
 .··············· 15分
.··············· 15分(1)设直线解析式为
 ,用待定系数法,由勾股定理得到点
,用待定系数法,由勾股定理得到点 ,而
,而 ,把它们代入即可
,把它们代入即可(2)关于
 对称,则对称轴
对称,则对称轴 ,再把点
,再把点 的坐标代入
的坐标代入 即可;由于点P关于直线AC的对称点在x轴上,利用直角三角形三角函数,得出直线
即可;由于点P关于直线AC的对称点在x轴上,利用直角三角形三角函数,得出直线 与
与 轴关于直线
轴关于直线 对称,则符合条件的点
对称,则符合条件的点 就是直线
就是直线 与抛物线
与抛物线 的交点,把
的交点,把 与
与 组成方程组,求方程组的解即可
组成方程组,求方程组的解即可(3)要求范围,要求边界值,即求PM+CM的最小值和最大值,当点
 的坐标是
的坐标是 时,则
时,则 ,故最小值为
,故最小值为 ,但没有最大值,故
,但没有最大值,故
 ;当
;当点
 的坐标是
的坐标是 时,把点
时,把点 和点
和点 分到
分到 轴的两侧,两点间连线最短,连线与
轴的两侧,两点间连线最短,连线与 轴的交点就点
轴的交点就点 ,
, 的最小值是
的最小值是 ,同样没有最大值,故
,同样没有最大值,故


练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 经过点O(0,0),A(4,0),B(5,5),点C是y轴负半轴上一点,直线
经过点O(0,0),A(4,0),B(5,5),点C是y轴负半轴上一点,直线 经过B,C两点,且
经过B,C两点,且 .
.
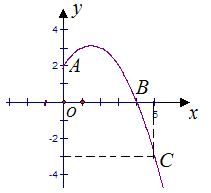
 ,对称轴
,对称轴 ,抛物线与
,抛物线与 轴两交点距离为4,求这个二次函数的解析式?
轴两交点距离为4,求这个二次函数的解析式? (元∕件)
(元∕件) (件)
(件)
 的图象与x轴必有两个交点.
的图象与x轴必有两个交点.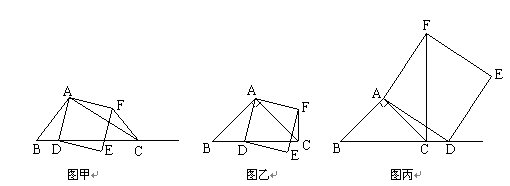
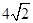 ,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值. 的图像过第一、三、四象限,则函数
的图像过第一、三、四象限,则函数 ( )
( )
