题目内容
一种成本为20元/件的新型商品经过40天试销售,发现销售量p(件)、销售单价q(元/件)与销售时间x(天)都满足一次函数关系,相关信息如图所示.
(1)试求销售量p(件)与销售时间x(天)的函数关系式;
(2)设第x天获得的利润为y元,求y关于x的函数关系式;
(3)求这40天试销售过程中何时利润最大?并求出最大值.
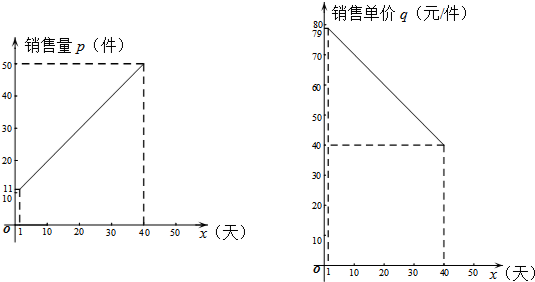
(1)试求销售量p(件)与销售时间x(天)的函数关系式;
(2)设第x天获得的利润为y元,求y关于x的函数关系式;
(3)求这40天试销售过程中何时利润最大?并求出最大值.

考点:二次函数的应用,一次函数的应用
专题:
分析:(1)直接利用待定系数法求一次函数解析式得出即可;
(2)直接利用待定系数法求一次函数解析式得出q=-x+80,再利用y=p(q-20)求出y与x的函数关系即可;
(3)直接利用配方法求出二次函数最值进而得出答案.
(2)直接利用待定系数法求一次函数解析式得出q=-x+80,再利用y=p(q-20)求出y与x的函数关系即可;
(3)直接利用配方法求出二次函数最值进而得出答案.
解答:解:(1)由图象可知:当1≤x≤40时,p是x的一次函数,设p=kx+b,
将(1,11)、(40,50)代入得:
,
解得:
∴当1≤x≤40时,p=x+10;
(2)由图象可知:当1≤x≤40时,q是x的一次函数,设q=k'x+b',
将(1,79)、(40,40)代入得:
,
解得:
∴当1≤x≤40时,q=-x+80.
由题意可知:当1≤x≤40时,
y=p (q-20)
=(x+10)(-x+80-20)
=-x2+50x+600;
(3)∵y=-x2+50x+600
=-(x-25)2+1225;
∴当x=25时,y取得最大值,最大值为1225.
即这40天试销过程中,第25天获得的利润最大,最大利润为1225元.
将(1,11)、(40,50)代入得:
|
解得:
|
∴当1≤x≤40时,p=x+10;
(2)由图象可知:当1≤x≤40时,q是x的一次函数,设q=k'x+b',
将(1,79)、(40,40)代入得:
|
解得:
|
∴当1≤x≤40时,q=-x+80.
由题意可知:当1≤x≤40时,
y=p (q-20)
=(x+10)(-x+80-20)
=-x2+50x+600;
(3)∵y=-x2+50x+600
=-(x-25)2+1225;
∴当x=25时,y取得最大值,最大值为1225.
即这40天试销过程中,第25天获得的利润最大,最大利润为1225元.
点评:此题主要考查了待定系数法求一次函数解析式以及二次函数最值求法,得出y与x的函数关系是解题关键.

练习册系列答案
相关题目
在函数y=
中,自变量x的取值范围是( )
| 1 | ||
|
| A、x>-5 | B、x≥-5 |
| C、x>0 | D、x≥0 |

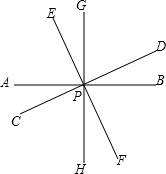 如图,直线AB、CD、EF和GH相交于点P,且∠APC=25°,∠EPG=25°,∠BPF=65°,问哪些直线互相垂直?为什么?
如图,直线AB、CD、EF和GH相交于点P,且∠APC=25°,∠EPG=25°,∠BPF=65°,问哪些直线互相垂直?为什么?