题目内容
4.已知△ABC∽△DEF,AB与DE的比为3:2,△ABC与△DEF的周长之差为5cm,求△ABC与△DEF的周长之和.分析 先根据相似三角形的性质求出△ABC与△DEF的周长之比,再根据△ABC与△DEF的周长之差为5cm即可得出两三角形的周长,进而可得出结论.
解答 解:∵△ABC∽△DEF,AB与DE的比为3:2,
∴$\frac{{C}_{△ABC}}{{C}_{△DEF}}$=$\frac{3}{2}$,
∴设△ABC的周长为3x,则△DEF的周长为2x.
∵△ABC与△DEF的周长之差为5cm,
∴3x-2x=5cm,解得x=5cm,
∴△ABC的周长为15cm,则△DEF的周长为10cm,
∴△ABC与△DEF的周长之和=15+10=25(cm).
答:△ABC与△DEF的周长之和为25cm.
点评 本题考查的是相似三角形的性质,熟知相似三角形周长的比等于相似比是解答此题的关键.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
9.若某二次函数的x与y的部分对应值如表:
(1)根据表格,试说明该函数图象的对称轴、顶点坐标和开口方向;
(2)当x为何值时,y随x的增大而增大;
(3)求出该函数的解析式.
| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -27 | -13 | -3 | 3 | 5 | 3 |
(2)当x为何值时,y随x的增大而增大;
(3)求出该函数的解析式.
 如图,在△ABC中,∠ACB=90°,DE垂直平分AC交AB于点D,交AC于点E,若∠A=30°,试判断△BCD的形状.并说明理由.
如图,在△ABC中,∠ACB=90°,DE垂直平分AC交AB于点D,交AC于点E,若∠A=30°,试判断△BCD的形状.并说明理由. 按图那样堆放钢管,第一层(最上层)有5根,第二层有6根,第三层有7根,…那么,第n层有多少根?并求出第30层钢管的根数.
按图那样堆放钢管,第一层(最上层)有5根,第二层有6根,第三层有7根,…那么,第n层有多少根?并求出第30层钢管的根数.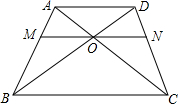 如图,已知梯形ABCD中,AD∥BC,AC,BD交于O,过O作AD的平行线交AB于M,交CD于N.若AD=3cm,BC=5cm,求ON.
如图,已知梯形ABCD中,AD∥BC,AC,BD交于O,过O作AD的平行线交AB于M,交CD于N.若AD=3cm,BC=5cm,求ON.