��Ŀ����
2����ͼ�ף���ƽ��ֱ������ϵ�У���G������Ϊ��0��4������G�������ύ��B��C��E��D�ĵ㣬��C������Ϊ��-4$\sqrt{3}$��0������ֱ��CM������BM�ӳ���x���ڵ�A������P�ӵ�O��ʼ��OA��ÿ��2$\sqrt{3}$����λ�����ٶ����A�ƶ�������Q�ӵ�A��ʼ��AB��ÿ��4����λ�����ٶ����B�ƶ������P��Q�ֱ��O��Aͬʱ�ƶ����ƶ�ʱ��Ϊt��0��t��6���룮��1�����G�İ뾶��A��B��������ꣻ
��2����tΪ��ֵʱ��PM���G���У�
��3����y�����Ƿ���ڵ�F��ʹ��FCMΪֱ�������Σ������ڣ������F�����ꣻ��������˵�����ɣ�
��4����ͼ�ң��Ƿ���ڡ�APQΪ���������Σ������ڣ������Ӧ��tֵ������������˵�����ɣ�

���� ��1����������������Ǻ���ֵ����á�GCO=30�㣬������������Ǻ���ֵ�����CG�ij��������ԲO�İ뾶��Ȼ����OB=OG+GB�����OB�ij����ʴ˿�֪��B�����꣬Ȼ���ڡ�AOB�У������OA�ij����ʴ˿�֪��A�����ꣻ
��2������CMP=90��ʱ����֤����CGO�ס�CPM�������������ε����ʿ����CP�ij���Ȼ������OP�ij����������OP=2$\sqrt{3}$t���з�����⼴�ɣ�
��3������M��F1M��CM����y�����F2������C��CF2��CM����y�����F2����������Ǻ���ֵ�������κ����Ķ������õ�F1��F2�����꣬��ֱ�����Ե�Բ�ܽ���90�㣬��֪����FΪԲ0��y��Ľ�������ʱ����CMFΪֱ�������Σ�Ȼ���ɵ�G�������Բ�İ뾶�����F3��F4�����ꣻ
��4����ΪAP=AQ��PQ=AQ��PA=PQ���������������ȵı�������Ǻ����г�����t�ķ�����⼴�ɣ�
��� �⣺��1���ߵ�G������Ϊ��0��4������C������Ϊ��-4$\sqrt{3}$��0����
��OG=4��OC=4$\sqrt{3}$��
��tan��GCO=$\frac{OG}{0C}$=$\frac{\sqrt{3}}{3}$��
���GCO=30�㣮
��CG=2OG=8����BGM=��CGO=60�㣮
���G�İ뾶Ϊ8��
��OB=OG+BG=+8=12��
��B��0��12����
��GB=GM����BGM=��CGO=60�㣮
���GBMΪ�ĵȱ������Σ�
���OBA=60�㣮
��$\frac{OA}{OB}=\sqrt{3}$����$\frac{OA}{12}=\sqrt{3}$����ã�OA=12$\sqrt{3}$��
��A��12$\sqrt{3}$��0����
��2������CMP=90��ʱ��PM���G���У�
�ߡ�CMP=��COG����GCO=��MCP��
���CGO�ס�CPM��
��$\frac{CG}{CP}=\frac{OC}{CM}$����$\frac{8}{CP}=\frac{4\sqrt{3}}{16}$����ã�CP=$\frac{32\sqrt{3}}{3}$��
��OP=CP-OC=$\frac{32\sqrt{3}}{3}$-4$\sqrt{3}$=$\frac{20\sqrt{3}}{3}$��
��2$\sqrt{3}$t=$\frac{20\sqrt{3}}{3}$����ã�t=$\frac{10}{3}$��
��t=$\frac{10}{3}$ʱ��ʱ��PM���G���У�
��3����ͼ1��ʾ������M��F1M��CM����y�����F2������C��CF2��CM����y�����F2��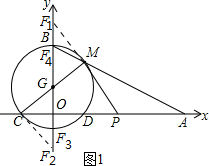
�١�F1M��CM��
���F1MG=90�㣬��F1GM=60�㣮
��GF1=2GM=16��
��OF1=OG+GF1=4+16=20��
��F1��0��20����
�ڡ�F2C��CM��
���F2CG=90�㣬��F2GC=60�㣮
��GF2=2GC=16��
��OF2=GF2-OG=16-4=12��
��F2��0��-12����
����ֱ�����Ե�Բ�ܽǵ���90���֪��CF3M=��CF4M=90��
��OF3=GF3-OG=8-4=4��
��F3��0��-4����
��OF4=OG+GF4=4+8=12��
��F4��0��12����
����������F��������0��20����0��-12����0��-4����0��12����
��4���ٵ�AP=AQʱ��
��AQ=4t��PA=OA-OP=12$\sqrt{3}$-2$\sqrt{3}$t��
��4t=12$\sqrt{3}$-2$\sqrt{3}t$��
��ã�t=12$\sqrt{3}$-18��
�ڵ�PQ=AQʱ����ͼ2��ʾ������Q��QE��AP������ΪE��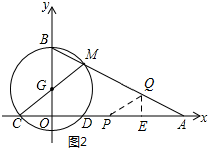
��PQ=AQ��QE��AP��
��PE=EA��
��AE=$\frac{1}{2}��$��12$\sqrt{3}$-2$\sqrt{3}$t��=6$\sqrt{3}$-$\sqrt{3}$t��
��$\frac{AE}{AQ}$=$\frac{\sqrt{3}}{2}$��
��$\frac{6\sqrt{3}-\sqrt{3}t}{4t}$=$\frac{\sqrt{3}}{2}$����ã�t=2��
����ͼ3��ʾ����PA=PQʱ��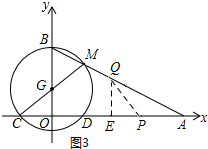
��QA=4t����A=30�㣬
��QE=2t��AE=2$\sqrt{3}$t��
��QP=PA����A=30�㣬
���QPE=60�㣮
��$\frac{QE}{QP}$=$\frac{\sqrt{3}}{2}$����$\frac{2t}{12\sqrt{3}-2\sqrt{3}t}$=$\frac{\sqrt{3}}{2}$����ã�t=3.6��
������������t=12$\sqrt{3}$-18��t=2��t=3.6ʱ����APQΪ���������Σ�
���� ������Ҫ�������Բ���ۺ�Ӧ�ã��������ҪӦ��������������Ǻ���ֵ���ȱ������ε����ʺ��ж������������ε����ʺ��ж������������ε����ʡ�Բ�ܽǶ�����֪ʶ�㣬��������������Ǻ���ֵ�г�����t�ķ����ǽ���Ĺؼ���

| A�� | 37��104 | B�� | 3.7��104 | C�� | 37��105 | D�� | 3.7��105 |
| A�� | a��2 | B�� | a��2 | C�� | a��2 | D�� | a��-2 |
 ��ͼ����֪AB��CD��CEƽ�֡�ACD����A����ACD=4��1�����ECD=18�㣮
��ͼ����֪AB��CD��CEƽ�֡�ACD����A����ACD=4��1�����ECD=18�㣮 ��ͼ����һ�ž���ֽƬ������AB=1��BC=2�������۵�����ֽƬ�������ҵ�AB���ϵĻƽ�ָ
��ͼ����һ�ž���ֽƬ������AB=1��BC=2�������۵�����ֽƬ�������ҵ�AB���ϵĻƽ�ָ