题目内容
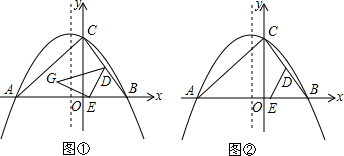
4. 中国机器人创意大赛于2014年7月15日在哈尔滨开幕.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m处往东一拐,仅走0.5m就到达了B.问机器人从点A到点B之间的距离是多少?
中国机器人创意大赛于2014年7月15日在哈尔滨开幕.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m处往东一拐,仅走0.5m就到达了B.问机器人从点A到点B之间的距离是多少?
分析 过点B作BC⊥AD于C,则△ABC为直角三角形,读图可以计算出AC.BC的长度,在直角△ABC中已知AC,BC,根据勾股定理即可计算AB.
解答 解:过点B作BC⊥AD于C,
从图中可以看出AC=4-2+0.5=2.5m,
BC=4.5+1.5=6m,
在直角△ABC中,AB为斜边,
则AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\frac{13}{2}$m.
答:机器人从点A到点B之间的距离是$\frac{13}{2}$m.
点评 本题考查了勾股定理在实际生活中的应用,考查了学生的读图能力,本题中正确的读图读出AC,BC的长度是解题的关键.

练习册系列答案
相关题目
15. 如图,在△ABC中,AD⊥BC于点D,AB+BD=CD,∠C=25°,则∠B等于( )
如图,在△ABC中,AD⊥BC于点D,AB+BD=CD,∠C=25°,则∠B等于( )
 如图,在△ABC中,AD⊥BC于点D,AB+BD=CD,∠C=25°,则∠B等于( )
如图,在△ABC中,AD⊥BC于点D,AB+BD=CD,∠C=25°,则∠B等于( )| A. | 25° | B. | 30° | C. | 50° | D. | 60° |
12.实数0,-π,$\sqrt{16}$,0.1010010001…(相邻两个1之间依次多一个0),$\frac{22}{7}$,-$\sqrt{5}$,其中无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.如图给出了四组三角形,其中全等的三角形有( )组.


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,顶点D恰好落在双曲线y=$\frac{y}{x}$.若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )
如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,顶点D恰好落在双曲线y=$\frac{y}{x}$.若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )