题目内容
14.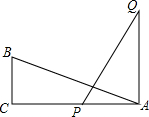 如图,△ABC中,∠C=90°,BC=4,AQ⊥AC,AQ=10,PQ⊥AB,且PQ=AB,则PC的长为6.
如图,△ABC中,∠C=90°,BC=4,AQ⊥AC,AQ=10,PQ⊥AB,且PQ=AB,则PC的长为6.
分析 利用已知条件证明△ABC≌△APQ,得到CA=AQ,BC=PA,根据PC=AC-AP=AQ-BC,即可解答.
解答 解:如图,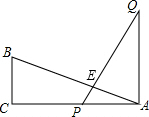
∵AQ⊥AC,PQ⊥AB,
∴∠QEA=∠PAQ=90°,
∵∠Q+∠QAE=90°,∠PAE+∠QAE=90°,
∴∠Q=∠PAE,
在△ABC和△APQ中,
$\left\{\begin{array}{l}{∠Q=∠PAE}\\{∠C=∠PAQ}\\{AB=PQ}\end{array}\right.$,
∴△ABC≌△APQ,
∴CA=AQ,BC=PA,
∴PC=AC-AP=AQ-BC=10-4=6.
故答案为:6.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是证明△ABC≌△APQ.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
19.数轴上原点以及原点右边的点所表示的数是( )
| A. | 负数 | B. | 非负数 | C. | 正数 | D. | 非正数 |
3.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
下列结论:①c=3;②当x>1时,y的值随x的增大而减小;③函数的最大值是5;④ac<0.其中正确的个数为 ( )
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |