题目内容
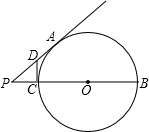 如图,P是⊙O直径BC延长线上的一点,PA与⊙O相切于A,CD⊥PB,且PC=CD,CD=3,则PB=________.
如图,P是⊙O直径BC延长线上的一点,PA与⊙O相切于A,CD⊥PB,且PC=CD,CD=3,则PB=________.
9+6
分析:首先证明CD是圆的切线,根据切线长定理和切线长定理即可求得PA的长,然后利用切割线定理即可求得PB的长.
解答:∵CD⊥PB,
∴CD是⊙O的切线,
又∵PA与⊙O相切于A,
∴AD=CD=3,
在直角△PCD中,PD= =3
=3 ,
,
∴PA=PD+AD=3 +3.
+3.
∵PA与⊙O相切于A,
∴PA2=PC•PB
∴PB= =
=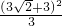 =9+6
=9+6 .
.
故答案是:9+6 .
.
点评:本题考查了切线长定理,切割线定理,以及切线的判定定理,正确求得PA的长度是解题的关键.

分析:首先证明CD是圆的切线,根据切线长定理和切线长定理即可求得PA的长,然后利用切割线定理即可求得PB的长.
解答:∵CD⊥PB,
∴CD是⊙O的切线,
又∵PA与⊙O相切于A,
∴AD=CD=3,
在直角△PCD中,PD=
 =3
=3 ,
,∴PA=PD+AD=3
 +3.
+3.∵PA与⊙O相切于A,
∴PA2=PC•PB
∴PB=
 =
=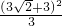 =9+6
=9+6 .
.故答案是:9+6
 .
.点评:本题考查了切线长定理,切割线定理,以及切线的判定定理,正确求得PA的长度是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
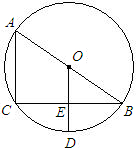 如图,AB是⊙O直径,BC是弦,OD⊥BC于E交弧BC于D.根据中考改编
如图,AB是⊙O直径,BC是弦,OD⊥BC于E交弧BC于D.根据中考改编 如图,AD是⊙O直径,∠AOC=100°,则∠D=
如图,AD是⊙O直径,∠AOC=100°,则∠D= (2012•惠城区模拟)如图,P是⊙0直径AB延长线上的点,PC切⊙0于C.若∠P=40°,则∠A的度数为
(2012•惠城区模拟)如图,P是⊙0直径AB延长线上的点,PC切⊙0于C.若∠P=40°,则∠A的度数为 (2012•荆州模拟)如图,AB是⊙0直径,C、D是
(2012•荆州模拟)如图,AB是⊙0直径,C、D是
 如图,AB是⊙O直径,∠AOC=140°,则∠D为( )
如图,AB是⊙O直径,∠AOC=140°,则∠D为( )