题目内容
已知抛物线y=2x2-4mx+
与x轴有两个不同的交点A、B,抛物线的顶点为C.
(1)当△ABC为等边三角形时,试确定点C的坐标;
(2)如何平移符合条件(1)的抛物线,使AC=
AB;
(3)设点D、E分别是AC、BC的中点,点F、G分别是DC、EC的中点,问四边形DFGE的面积S的大小与m的取值是否有关?若有关,写出其关系式;若无关,请说明理由.
| 1 |
| 2 |
(1)当△ABC为等边三角形时,试确定点C的坐标;
(2)如何平移符合条件(1)的抛物线,使AC=
| 3 |
| 2 |
(3)设点D、E分别是AC、BC的中点,点F、G分别是DC、EC的中点,问四边形DFGE的面积S的大小与m的取值是否有关?若有关,写出其关系式;若无关,请说明理由.
考点:二次函数综合题
专题:压轴题
分析:(1)利用根的判别式列出关于m的不等式,设抛物线与x轴的两个交点坐标分别为(x1,0)(x2,0),顶点坐标为(h,k),利用根与系数的关系表示出AB,h、k,再根据等边三角形的性质列出方程求解即可;
(2)用AB表示出k,然后列出方程求出m的值,从而得到顶点C的坐标,再求出原抛物线的顶点坐标,然后根据顶点的变化确定平移方法即可;
(3)根据三角形的中位线定理求出S△DCE=
S△ABC,S△FCG=
S△DCE,然后求出S四边形DFGE=
S△ABC,再根据三角形的面积公式列式整理即可得解.
(2)用AB表示出k,然后列出方程求出m的值,从而得到顶点C的坐标,再求出原抛物线的顶点坐标,然后根据顶点的变化确定平移方法即可;
(3)根据三角形的中位线定理求出S△DCE=
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 16 |
解答:解:(1)∵抛物线与x轴有两个不同的交点,
∴△=(-4m)2-4×2×
>0,
∴4m2-1>0,
设抛物线与x轴的两个交点坐标分别为(x1,0)(x2,0),顶点坐标为(h,k),
则AB=|x1-x2|=
=
,
h=-
=m,k=
=
,
∵△ABC为等边三角形,
∴|k|=
AB,
∴
=
×
,
∴m2=1,
解得m=±1,
当m=1时,h=1,k=-
,
当m=-1时,h=-1,k=-
,
所以,点C的坐标为(1,-
)或(-1,-
);
(2)由AC=
AB得,|k|=
AB,
所以
=
×
,
整理得m2=
,
解得m=±
,
所以,AB=
=2
,
|k|=
×2
=4,
k=-4,
∴平移后点C的坐标为(
,-4)或(-
,-4),
所以,应将(1)中C为(1,-
)的抛物线先向下平移
个单位,再向右平移
个单位,或向左平移
个单位;
将C为(-1,-
)的抛物线先向下平移
个单位,再向右平移
个单位,或向左平移
个单位;
(3)∵点D、E分别是AC、BC的中点,
∴S△DCE=
S△ABC,
∵点F、G分别是DC、EC的中点,
∴S△FCG=
S△DCE,
∴S四边形DFGE=
S△ABC,
∵S△ABC=
×
,
∴S=
×
×
=
(4m2-1)
,
∴四边形DFGE的面积S的大小与m的取值有关,
其关系式为S=
(4m2-1)
.
∴△=(-4m)2-4×2×
| 1 |
| 2 |
∴4m2-1>0,
设抛物线与x轴的两个交点坐标分别为(x1,0)(x2,0),顶点坐标为(h,k),
则AB=|x1-x2|=
(-
|
| 4m2-1 |
h=-
| -4m |
| 2×2 |
4×2×
| ||
| 4×2 |
| 1-4m2 |
| 2 |
∵△ABC为等边三角形,
∴|k|=
| ||
| 2 |
∴
| 4m2-1 |
| 2 |
| ||
| 2 |
| 4m2-1 |
∴m2=1,
解得m=±1,
当m=1时,h=1,k=-
| 3 |
| 2 |
当m=-1时,h=-1,k=-
| 3 |
| 2 |
所以,点C的坐标为(1,-
| 3 |
| 2 |
| 3 |
| 2 |
(2)由AC=
| 3 |
| 2 |
| 2 |
所以
| 4m2-1 |
| 2 |
| 2 |
| 4m2-1 |
整理得m2=
| 9 |
| 4 |
解得m=±
| 3 |
| 2 |
所以,AB=
4×(±
|
| 2 |
|k|=
| 2 |
| 2 |
k=-4,
∴平移后点C的坐标为(
| 3 |
| 2 |
| 3 |
| 2 |
所以,应将(1)中C为(1,-
| 3 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
将C为(-1,-
| 3 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
(3)∵点D、E分别是AC、BC的中点,
∴S△DCE=
| 1 |
| 4 |
∵点F、G分别是DC、EC的中点,
∴S△FCG=
| 1 |
| 4 |
∴S四边形DFGE=
| 3 |
| 16 |
∵S△ABC=
| 1 |
| 2 |
| 4m2-1 |
| 4m2-1 |
| 2 |
∴S=
| 3 |
| 16 |
| 1 |
| 2 |
| 4m2-1 |
| 4m2-1 |
| 2 |
| 3 |
| 64 |
| 4m2-1 |
∴四边形DFGE的面积S的大小与m的取值有关,
其关系式为S=
| 3 |
| 64 |
| 4m2-1 |
点评:本题是二次函数综合题型,主要利用了抛物线与x轴的交点问题,根与系数的关系,等边三角形的性质,三角形的中位线平行于第三边并且等于第三边的一半,表示出AB的长和顶点C的纵坐标是解题的关键,也是本题的难点.

练习册系列答案
相关题目
下列各数中,最小的数是( )
| A、-2 | B、-1 | C、0 | D、2 |
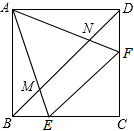 如图,正方形ABCD中,点E、F分别在BC、CD上,∠EAF=45°,AE、AF分别于BD相交于点M、N,
如图,正方形ABCD中,点E、F分别在BC、CD上,∠EAF=45°,AE、AF分别于BD相交于点M、N, 如图,AB、CD交于E,且AC=BD,∠A+∠B=180°,求证:CE=DE.
如图,AB、CD交于E,且AC=BD,∠A+∠B=180°,求证:CE=DE. 已知∠C=∠D=90°,E是CD上的一点,AE、BE分别平分∠DAB、∠ABC.求证:E是CD的中点.
已知∠C=∠D=90°,E是CD上的一点,AE、BE分别平分∠DAB、∠ABC.求证:E是CD的中点. 如图是小明用七巧板拼出的图案.
如图是小明用七巧板拼出的图案.