题目内容
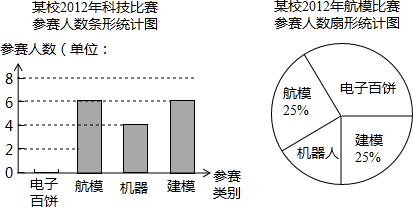
某服装厂现大A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装80套.已知做一套M型号的时装需要A种布料0.6米,B种布料0.9米,可获利45元,做一套N型号的时装需要A种布料1.1米,B种布料0.4米,可获利50元.若设生产N型号的时装套数为x,用这批布料生产这两种型号的时装所获的总利润为y元.
(1)求y与x的函数关系式,并求出自变量x的取值范围;
(2)该服装厂在生产这批时装中,当生产N型号的时装多少套时,所获利润最大?最大利润是多少?
(1)求y与x的函数关系式,并求出自变量x的取值范围;
(2)该服装厂在生产这批时装中,当生产N型号的时装多少套时,所获利润最大?最大利润是多少?
考点:一次函数的应用
专题:
分析:(1)由于计划用这两种布料生产M、N两种型号的时装共80套,设生产N型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元,做一套N型号的时装可获利50元;做一套M型号的时装 可获利45元,由此即可求解;
(2)进一步根据一次函数的增减性求出所获利润最大值即可.
(2)进一步根据一次函数的增减性求出所获利润最大值即可.
解答:解:(1)设生产N型号的时装套数为x,则生产M型号的时装为(80-x),由题意,得
y=50x+45(80-x)=5x+3600;
(2)由题意得
,
解得不等式组的解集是40≤x≤44,
∵x为整数,
∴x=40,41,42,43,44,
∴y与x的函数关系式是y=5x+3600(x=40,41,42,43,44);
∵k=5>0,
∴y随x的增大而增大,
∴当x=44时,y最大=3820,
即生产N型号的时装44套时,该厂所获利润最大,最大利润是3820元.
y=50x+45(80-x)=5x+3600;
(2)由题意得
|
解得不等式组的解集是40≤x≤44,
∵x为整数,
∴x=40,41,42,43,44,
∴y与x的函数关系式是y=5x+3600(x=40,41,42,43,44);
∵k=5>0,
∴y随x的增大而增大,
∴当x=44时,y最大=3820,
即生产N型号的时装44套时,该厂所获利润最大,最大利润是3820元.
点评:本题考查了一次函数的应用,一元一次不等式组的应用,利用一次函数求最值时,关键是应用一次函数的性质:即由函数y随x的变化,结合自变量的取值范围确定最值.

练习册系列答案
相关题目

 如图,已知点A、B是⊙O外两个相异的点,点P在⊙O上,PA、PB分别与圆O交于异于点P的点D、C,且AD•AP=BC•BP.
如图,已知点A、B是⊙O外两个相异的点,点P在⊙O上,PA、PB分别与圆O交于异于点P的点D、C,且AD•AP=BC•BP.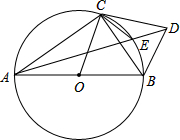 如图,过Rt△ABC的直角顶点C作它的外接⊙O的切线CD,BD⊥CD,D是垂足,AD交⊙O于E.求证:
如图,过Rt△ABC的直角顶点C作它的外接⊙O的切线CD,BD⊥CD,D是垂足,AD交⊙O于E.求证: