题目内容
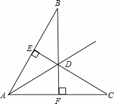
如图1,在等腰三角形ABC中,AB=AC,在底边BC上取一点D,在边AC上取一点E,使AE=AD,连接DE,在∠ABD的内部作∠ABF=2∠EDC,交AD于点F.
(1)求证:△ABF是等腰三角形;
(2)如图2,BF的延长交AC于点G.若∠DAC=∠CBG,延长AC至点M,使GM=AB,连接BM,点N是BG的中点,连接AN,试判断线段AN、BM之间的数量关系,并证明你的结论.
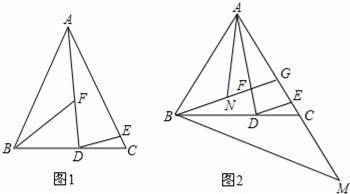

【考点】全等三角形的判定与性质;等腰三角形的判定与性质.
【分析】(1)先利用等腰三角形ABC,得出∠ABD=∠ACD,再利用三角形外角定理得出∠BAD+∠ABD=∠ADE+∠EDC,∠EDC+∠ACD=∠AED,再结合∠ABF=2∠EDC,即可求出结论.
(2)延长CA至点H,使AG=AH,连接BH,由三角形中位线定理得出AG=
 BH,再得出△ABC是等边三角形,易证△BAH≌△BCM,可得出BH=BM,即可得出结论AG=
BH,再得出△ABC是等边三角形,易证△BAH≌△BCM,可得出BH=BM,即可得出结论AG=
 BM.
BM.
【解答】解:(1)∵等腰三角形ABC中,AB=AC,
∴∠ABD=∠ACD,
∵∠BAD+∠ABD=∠ADE+∠EDC,∠EDC+∠ACD=∠AED,
∵AE=AD,
∴∠ADE=∠AED,
∴∠BAD=2∠EDC,
∵∠ABF=2∠EDC,
∴∠BAD=∠ABF,
∴△ABF是等腰三角形;
(2)如图2延长CA至点H,使AG=AH,连接BH,
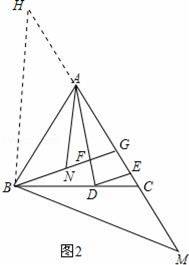

∵点N是BG的中点,
∴AN=
 BH,
BH,
∵∠BAD=∠ABF(1)中已证明,∠DAC=∠CBG,
∴∠CAB=∠CBA,
∴△ABC是等边三角形,
∴AB=BC=AC,
∠BAC=∠BCA=60°,
∵GM=AB,AB=AC,
∴CM=AG,
∴AH=CM,
在△BAH和△BCM中,
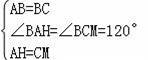

∴△BAH≌△BCM(SAS),
∴BH=BM,
∴AN=
 BM.
BM.
【点评】本题主要考查了全等三角形的判定和性质及等腰三角形的判定与性质,解题的关键是正确作出辅助线,得出第(2)题中△ABC是等边三角形.

 快捷英语周周练系列答案
快捷英语周周练系列答案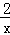 ,下列说法不正确的是( )
,下列说法不正确的是( )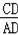
 =
=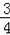
 ,求cos∠DAB.
,求cos∠DAB.


 的值,其中a=tan60°﹣6sin30°.
的值,其中a=tan60°﹣6sin30°. ,AB=AC,BD平分∠ABC,∠A=36°,则∠1的度数为( )
,AB=AC,BD平分∠ABC,∠A=36°,则∠1的度数为( )
 = .
= . 点D在∠BAC的平分线上.
点D在∠BAC的平分线上.