题目内容
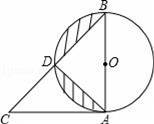
如图所示,已知BD=CD,BF⊥AC,CE⊥AB,求证: 点D在∠BAC的平分线上.
点D在∠BAC的平分线上.
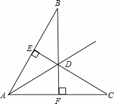 |
证明:∵BF⊥AC,CE⊥AB,∴∠BED=∠CFD=90o
在△BED和△CDF中

 ∴△BDE≌△CFD(AAS)
∴△BDE≌△CFD(AAS)
∴ED=FD,
又∵BF⊥AC,CE⊥AB
∴点D在∠BAC的平分线上
即AD是∠BAC的平分线,

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)如图1,请你写出AB与AP所满足的数量关系和位置关系(不必证明);
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点O,连接AP,BO.猜想并写出BO与AP所满足的数量关系和位置关系,并说明理由;

| |

 (3)将△EFP沿直线l继续向左平移到图3的位置时,EP的延长线交AC的延长线于点O,连接AP,BO.此时,BO与AP还具有(2)中的数量关系和位置关系吗?请说明
(3)将△EFP沿直线l继续向左平移到图3的位置时,EP的延长线交AC的延长线于点O,连接AP,BO.此时,BO与AP还具有(2)中的数量关系和位置关系吗?请说明 理由.
理由. 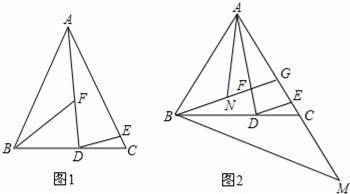


 ,
, ,
, 的最简公分母为( )
的最简公分母为( )
 D. 16
D. 16
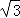 ,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )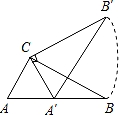
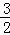 π B.
π B.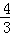
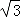 π C.2π D.3π
π C.2π D.3π