题目内容
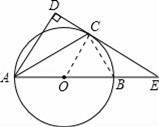
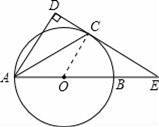
如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.
(1)求证:CD为⊙O的切线.
(2)若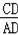
 =
=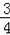
 ,求cos∠DAB.
,求cos∠DAB.


【考点】切线的判定;角平分线的性质;勾股定理;解直角三角形.
【专题】几何综合题.
【分析】(1)连接OC,推出∠DAC=∠CAB,∠OAC=∠OCA,求出∠DAC=∠OCA,得出OC∥AD,推出OC⊥DC,根据切线的判定判断即可;
(2)连接BC,可证明△ACD∽△ABC,得出比例式,求出BC,求出圆的直径AB,再根据勾股定理得出CE,即可求出答案.
【解答】(1)证明:连接OC,
∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵OC=OA,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∵OC为⊙O半径,
∴CD是⊙O的切线;
(2)解:连接BC,
∵AB为直径,
∴∠ACB=90°,
∵AC平分∠BAD,
∴∠CAD=∠CAB,
∵
 =
=
 ,
,
∴令CD=3,AD=4,得AC=5,
∴
 =
=
 ,
,
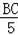
 =
=
 ,
,
∴BC=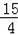
 ,
,
由勾股定理得AB=
 ,
,
∴OC=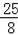
 ,
,
∵OC∥AD,
∴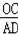
 =
=
 ,
,
∴
 =
=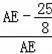
 ,
,
解得AE=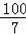
 ,
,
∴cos∠DAB=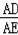
 =
=
 =
=
 .
.


【点评】本题考查了切线的判定以及角平分线的定义、勾股定理和解直角三角形,是中学阶段的重点内容.

练习册系列答案
相关题目

 cm,在圆柱体下底面A点有一只蚂蚁,想吃到上底面B点的一粒砂糖(A、B是圆柱体上、下底面相对的两点),则这只蚂蚁从A出点沿着圆柱表面爬到B点的最短路线的长是__________.
cm,在圆柱体下底面A点有一只蚂蚁,想吃到上底面B点的一粒砂糖(A、B是圆柱体上、下底面相对的两点),则这只蚂蚁从A出点沿着圆柱表面爬到B点的最短路线的长是__________.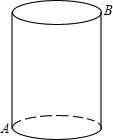




 =
=
 ,若AE=5,则EC的长度为( )
,若AE=5,则EC的长度为( )