��Ŀ����
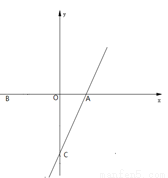
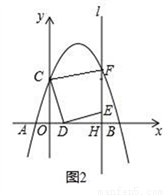
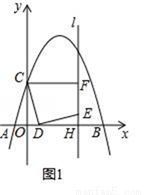
��ͼ1����ƽ��ֱ������ϵ�У�������y=ax2+bx+3��x����A����1��0����B��5��0�����㣬��y���ڵ�C����D���߶�OB��һ���㣬����CD�����߶�CD�Ƶ�D˳ʱ����ת90��õ��߶�DE������E��ֱ��l��x����H�����������ڵ�M������C��CF��l��F��
��1���������߽���ʽ��
��2����ͼ2������Fǡ������������ʱ�����M�غϣ�
�����F�����ꣻ
�����߶�OD�ij���
����̽����ֱ��l�ϣ��Ƿ���ڵ�G��ʹ��EDG=45�㣿�����ڣ���ֱ��д����G�����ꣻ�������ڣ���˵�����ɣ�
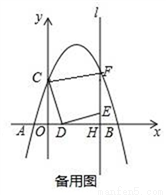
��3���ڵ�D���˶������У�����CM������COD�ס�CFM����ֱ��д���߶�OD�ij���
��ϰ��ϵ�д�
 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
�����Ŀ



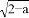 �������a��ȡֵ��Χ�ǣ� ��
�������a��ȡֵ��Χ�ǣ� ��
 ��ͼ������ɺ���
��ͼ������ɺ��� ��ͼ��( )�õ�
��ͼ��( )�õ�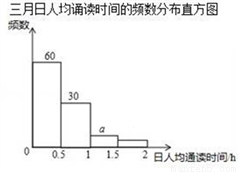
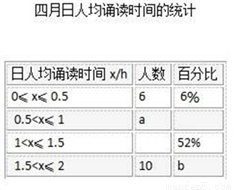
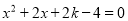 ��
��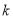 ��ȡֵ��Χ��
��ȡֵ��Χ��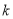 ֵ��������̵����������ʵ������
ֵ��������̵����������ʵ������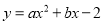 ��ͼ��
��ͼ��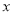 ����
����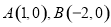 ����
���� ���ڵ�
���ڵ�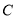 ������ֱ��
������ֱ��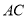 .
.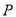 �ڶ��κ�����ͼ���ϣ�Բ
�ڶ��κ�����ͼ���ϣ�Բ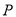 ��ֱ��
��ֱ��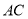 ���У��е�Ϊ
���У��е�Ϊ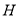 .
.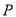 ��
��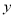 �����࣬�ҡ�
�����࣬�ҡ�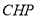 �ס�
�ס�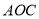 �����
�����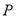 �����ꣻ
�����ꣻ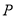 �İ뾶Ϊ4�����
�İ뾶Ϊ4�����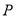 ������.
������.