题目内容
14.求证:矩形的四个角的平分线所围成的四边形是正方形.分析 首先根据已知条件证明四边形EMFN是矩形,再根据正方形的判定:邻边相等的矩形是正方形即证明FM=EM即可.
解答 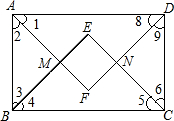 如图,在矩形ABCD中,AF、BE、CE、DF分别是矩形的四个角的角平分线,E、M、F、N是其交点,
如图,在矩形ABCD中,AF、BE、CE、DF分别是矩形的四个角的角平分线,E、M、F、N是其交点,
求证:四边形EMFN是正方形.
证明:∵四边形ABCD是矩形,
∴四个内角均为90°,
∵AF,BE,CE,DF分别是四个内角的平分线,
∴∠EBC=∠ECB=45°,
∴△EBC为等腰直角三角形,
∴∠E=90°,
同理∠F=∠EMF=∠ENF=90°,
∴四边形MFNE为矩形,
∵$\left\{\begin{array}{l}{∠F=∠E}\\{∠1=∠4}\\{AD=BC}\end{array}\right.$,
∴△DAF≌△CBE(AAS)
∴AF=BE,
∵AM=BM,
∴AF-AM=BE-BM,即FM=EM,
∴四边形MFNE是正方形.
点评 本题考查了矩形的性质和判定、角平分线的性质等腰直角三角形的判定和性质以及正方形的判定,解题的关键是对特殊的几何图形的判定和性质要熟练掌握.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
2. 如图,直线AB,CD相交于点O,EO⊥AB,垂直为点O,∠BOD=50°,则∠COE=( )
如图,直线AB,CD相交于点O,EO⊥AB,垂直为点O,∠BOD=50°,则∠COE=( )
 如图,直线AB,CD相交于点O,EO⊥AB,垂直为点O,∠BOD=50°,则∠COE=( )
如图,直线AB,CD相交于点O,EO⊥AB,垂直为点O,∠BOD=50°,则∠COE=( )| A. | 30° | B. | 140° | C. | 50° | D. | 60° |
4.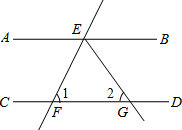 如图,AB∥CD,EF交AB于点E,交CD于点F,EG平分∠BEF交CD于点G.若∠1=40°,则∠2的度数是( )
如图,AB∥CD,EF交AB于点E,交CD于点F,EG平分∠BEF交CD于点G.若∠1=40°,则∠2的度数是( )
 如图,AB∥CD,EF交AB于点E,交CD于点F,EG平分∠BEF交CD于点G.若∠1=40°,则∠2的度数是( )
如图,AB∥CD,EF交AB于点E,交CD于点F,EG平分∠BEF交CD于点G.若∠1=40°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |