题目内容
8.已知三角形两边的长分别是2和8,则此三角形第三边的长可能是( )| A. | 5 | B. | 6 | C. | 7 | D. | 11 |
分析 已知三角形的两边长分别为2和8,根据在三角形中任意两边之和>第三边,任意两边之差<第三边;即可求第三边长的范围.
解答 解:设第三边长为x,则由三角形三边关系定理得8-2<x<8+2,即6<x<10.
因此,本题的第三边应满足6<x<10,把各项代入不等式符合的即为答案.
只有7符合不等式,
故选C.
点评 本题考查的是三角形的三边关系,即任意两边之和大于第三边,任意两边之差小于第三边.

练习册系列答案
相关题目
3.下列计算正确的是( )
| A. | $\sqrt{{{(-3)}^2}}=-3$ | B. | $\sqrt{{3^2}+{4^2}}=7$ | C. | $\sqrt{(-4)×(-9)}=\sqrt{4}×\sqrt{9}=6$ | D. | $\sqrt{4\frac{1}{4}}=2\frac{1}{2}$ |
13.某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4290元,且销售完这批商品后获利多于1260元,请问共有几种购货方案?
| 甲 | 乙 | |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
(2)若商店计划投入资金少于4290元,且销售完这批商品后获利多于1260元,请问共有几种购货方案?
18.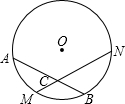 如图所示,M是弧AB的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=4$\sqrt{3}$cm,则∠ACM的度数是( )
如图所示,M是弧AB的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=4$\sqrt{3}$cm,则∠ACM的度数是( )
 如图所示,M是弧AB的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=4$\sqrt{3}$cm,则∠ACM的度数是( )
如图所示,M是弧AB的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=4$\sqrt{3}$cm,则∠ACM的度数是( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
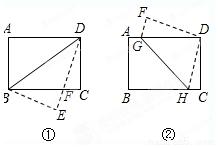 在矩形纸片ABCD中,AB=6,BC=8,
在矩形纸片ABCD中,AB=6,BC=8,