题目内容
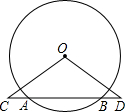如图，已知⊙O，线段CD与⊙O交于A，B两点，且OC=OD．试比较线段AC和BD的大小，并说明理由．
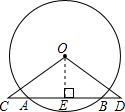解：线段AC=BD．理由如下：如图，过O作OE⊥CD，点E为垂足，
∵OE⊥AB，
∴EA=EB，
又∵OC=OD，OE⊥CD，
∴CE=DE，
∴AC=BD．
分析：过O作OE⊥CD，点E为垂足，而OC=OD，则EA=EB，CE=DE，所以AC=BD．
点评：本题考查了垂径定理（垂直于弦的直径平分弦）以及等腰三角形的性质．
练习册系列答案
相关题目
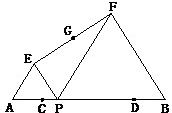8、如图：已知P是线段AB上的动点（P不与A，B重合），分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB，连接EF，设EF的中点为G；点C、D在线段AB上且AC=BD，当点P从点C运动到点D时，设点G到直线AB的距离为y，则能表示y与P点移动的时间x之间函数关系的大致图象是（ ）
如图，已知AB是线段CD的垂直平分线，E是AB上的一点，如果∠ECD=55°，那么下列说法错误的是（ ）
尺规作图：（要求：不写作法，但要保留作图痕迹）
如图，已知⊙O，线段AB与⊙O交于C、D两点，且OA=OB，
如图，已知DE由线段AB平移得到的，且AB=DC=4cm，EC=3cm，则△DCE的周长是（ ）