题目内容
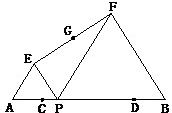 8、如图:已知P是线段AB上的动点(P不与A,B重合),分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连接EF,设EF的中点为G;点C、D在线段AB上且AC=BD,当点P从点C运动到点D时,设点G到直线AB的距离为y,则能表示y与P点移动的时间x之间函数关系的大致图象是( )
8、如图:已知P是线段AB上的动点(P不与A,B重合),分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连接EF,设EF的中点为G;点C、D在线段AB上且AC=BD,当点P从点C运动到点D时,设点G到直线AB的距离为y,则能表示y与P点移动的时间x之间函数关系的大致图象是( )分析:分别延长AE,BF交于点H,则可证得四边形EPFH为平行四边形,利用平行四边形的性质:对角线相互平分,可得G为EF的中点,也是PH的中点,所以G的运动轨迹是三角形HCD的中位线,所以点G到直线AB的距离为y是一个定值,问题得解.
解答:解: 如图分别延长AE,BF交于点H,
如图分别延长AE,BF交于点H,
∵∠A=∠FPB=60°,
∴AH∥PF,
∵∠B=∠EPA=60°,
∴BH∥PE,
∴四边形EPFH为平行四边形,
∴EF与HP互相平分,
∴G为HP的中点,
∵EF的中点为G,
∴P从点C运动到点D时,G始终为PH的中点,
∴G运动的轨迹是三角形HCD的中位线MN,
又∵MN∥CD,
∴G到直线AB的距离为一定值,
∴y与P点移动的时间x之间函数关系的大致图象是一平行于y轴的射线(x≥0).
故选D.
 如图分别延长AE,BF交于点H,
如图分别延长AE,BF交于点H,∵∠A=∠FPB=60°,
∴AH∥PF,
∵∠B=∠EPA=60°,
∴BH∥PE,
∴四边形EPFH为平行四边形,
∴EF与HP互相平分,
∴G为HP的中点,
∵EF的中点为G,
∴P从点C运动到点D时,G始终为PH的中点,
∴G运动的轨迹是三角形HCD的中位线MN,
又∵MN∥CD,
∴G到直线AB的距离为一定值,
∴y与P点移动的时间x之间函数关系的大致图象是一平行于y轴的射线(x≥0).
故选D.
点评:本题考查了动点问题的函数图象,利用到的是三角形的中位线定理:三角形的中位线平行且等于第三边的一半.对于此类问题来说是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.用图象解决问题时,要理清图象的含义即会识图.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
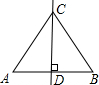 如图,已知CD是线段AB的垂直平分线,垂足为D,E是CD上一点.若∠A=60°,则下列结论中错误的是( )
如图,已知CD是线段AB的垂直平分线,垂足为D,E是CD上一点.若∠A=60°,则下列结论中错误的是( )| A、AE=BE | B、AD=BD | C、AB=AC | D、ED=AD |
如图,已知C是线段AB的中点,则CD等于( )


| A、AD-BD | ||
B、
| ||
C、
| ||
D、AD-
|
 如图,已知B是线段AE上一点,ABCD和BEFG都是正方形,连接AG、CE.
如图,已知B是线段AE上一点,ABCD和BEFG都是正方形,连接AG、CE. (2012•宿迁)如图,已知P是线段AB的黄金分割点,且PA>PB,若S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1
(2012•宿迁)如图,已知P是线段AB的黄金分割点,且PA>PB,若S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1