��Ŀ����
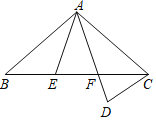
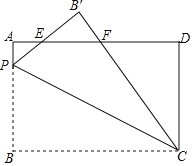
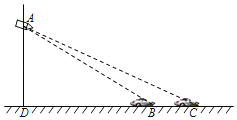
����Ŀ����ͼ��һ���γ��ھ���ij·�ڵĸ�Ӧ��B��C��ʱ�����۵Ƹ��ϵĵ��Ӿ������㵽������Ƭ������Ӧ��֮�����BCΪ6m���ڸ�Ӧ��B��C������õ��Ӿ���A�����Ƿֱ�Ϊ��ABD��18������ACD��14��������Ӿ��찲װ�����۵Ƹ��ϵĸ߶�AD�ij���
���ο����ݣ�sin14���0.242��cos14���0.97��tan14���0.25��sin18���0.309��cos18���0.951��tan18���0.325��
���𰸡�AD�ij�Ϊ6.5 m��
��������
����Ӿ��찲װ�����۵Ƹ��ϵĸ߶�AD�ij�Ϊxm��ͨ����Rt��ADB��Rt��ACD���BD��CD�ij��ȣ�Ȼ����BC��CD��BD�г����̣������
����Ӿ��찲װ�����۵Ƹ��ϵĸ߶�AD�ij�Ϊx m��
��Rt��ADB��tan��ABD��![]() ��
��
��BD��![]() ��
��
��Rt��ACD��tan��ACD�� ![]() ��
��
��CD��![]() ��
��
��BC��CD��BD��
��![]() ��
��![]() ��6��
��6��
��4x��![]() x��6��
x��6��
��������̣���x��6.5��
�𣺵��Ӿ��찲װ�����۵Ƹ��ϵĸ߶�AD�ij�Ϊ6.5 m��

 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�����Ŀ���ס�������ͬѧ�ֱ����6�����ѵ����ѵ���ɼ�����λ���������±�
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | |
�� | 9 | 8 | 6 | 7 | 8 | 10 |
�� | 8 | 7 | 9 | 7 | 8 | 8 |
�����ǵ�ѵ���ɼ������·���������˵����ȷ���ǣ�������
A. ����ѵ���ɼ���ƽ������ͬ B. ����ѵ���ɼ�����λ����ͬ
C. ����ѵ���ɼ���������ͬ D. ����ѵ���ɼ��ķ��ͬ