题目内容
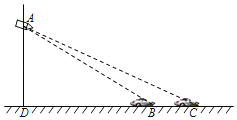
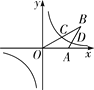
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (k≠0)的图象经过等腰△AOB底边OB的中点C和AB边上一点D,已知A(4,0),∠AOB=30°,则k的值为( )
(k≠0)的图象经过等腰△AOB底边OB的中点C和AB边上一点D,已知A(4,0),∠AOB=30°,则k的值为( )
A.2![]() B.3
B.3![]() C.3D.4
C.3D.4
【答案】B
【解析】
过点B作BE⊥x轴于点E,然后利用特殊角的三角函数值求出点B的坐标,进而点C的坐标可求,然后将点C代入反比例函数中即可求出k的值.
如解图,过点B作BE⊥x轴于点E,

∵A(4,0),OA=OB,
∴OA=AB=4,
∴∠AOB=∠ABO=30°,
∴∠BAE=2∠AOB=60°,
∴BE=AB·sin∠BAE=4×![]() =2
=2![]() ,AE=AB·cos∠BAE=4×
,AE=AB·cos∠BAE=4×![]() =2,
=2,
∴OE=OA+AE=4+2=6,
∴点B的坐标为(6,2![]() ),
),
∵点C为OB中点,
∴点C的坐标为(3,![]() ),
),
又∵反比例函数y=![]() (k≠0)的图象经过点C,
(k≠0)的图象经过点C,
∴k=3×![]() =3
=3![]() .
.
故选:B.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
【题目】某品牌电脑销售公司有营销员14人,销售部为制定营销人员月销售电脑定额,统计了这14人某月的销售量如下(单位:台):
销售量 | 200 | 170 | 130 | 80 | 50 | 40 |
人数 | 1 | 1 | 2 | 5 | 3 | 2 |
(1)该公司营销员销售该品牌电脑的月销售平均数是 台,中位数是 台,众数是 台.
(2)销售部经理把每位营销员月销售量定为90台,你认为是否合理?说明理由.