题目内容
计算:
①(2x-3y)2-8y2;
②(m+3n)(m-3n)-(m-3n)2;
③(a-b+c)(a-b-c);
④(x+2y-3)(x-2y+3);
⑤(a-2b+c)2;
⑥[(x-2y)2+(x-2y)(2y-x)-2x(2x-y)]÷2x.
⑦(m+2n)2(m-2n)2
⑧(
a+
b+
c)2-(
a-
b-
c)2.
①(2x-3y)2-8y2;
②(m+3n)(m-3n)-(m-3n)2;
③(a-b+c)(a-b-c);
④(x+2y-3)(x-2y+3);
⑤(a-2b+c)2;
⑥[(x-2y)2+(x-2y)(2y-x)-2x(2x-y)]÷2x.
⑦(m+2n)2(m-2n)2
⑧(
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
考点:整式的混合运算
专题:计算题
分析:①原式利用完全平方公式展开,去括号合并即可得到结果;
②原式第一项利用平方差公式计算,第二项利用完全平方公式展开,去括号合并即可得到结果;
③原式利用平方差公式化简,再利用完全平方公式展开即可得到结果;
④原式利用平方差公式化简,再利用完全平方公式展开即可得到结果;
⑤原式利用完全平方公式展开,即可得到结果;
⑥原式中括号中利用完全平方公式化简,去括号合并后利用多项式除以单项式法则计算即可得到结果;
⑦原式逆用积的乘方运算法则变形,计算即可得到结果;
⑧原式利用平方差公式计算即可得到结果.
②原式第一项利用平方差公式计算,第二项利用完全平方公式展开,去括号合并即可得到结果;
③原式利用平方差公式化简,再利用完全平方公式展开即可得到结果;
④原式利用平方差公式化简,再利用完全平方公式展开即可得到结果;
⑤原式利用完全平方公式展开,即可得到结果;
⑥原式中括号中利用完全平方公式化简,去括号合并后利用多项式除以单项式法则计算即可得到结果;
⑦原式逆用积的乘方运算法则变形,计算即可得到结果;
⑧原式利用平方差公式计算即可得到结果.
解答:解:①原式=4x2-12xy+9y2-8y2=4x2-12xy+y2;
②原式=m2-9n2-m2+6mn-9n2=6mn-18n2;
③原式=(a-b)2-c2=a2-2ab+b2-c2;
④原式=x2-(2y-3)2=x2-4y2+12y-9;
⑤原式=(a-2b)2+2c(a-2b)+c2=a2-4ab+4b2+2ac-4bc+c2;
⑥原式=(x2-4xy+4y2-x2+4xy-4y2-4x2+2xy)÷2x=(-4x2+2xy)÷2x=-2x+y;
⑦原式=[(m+2n)(m-2n)]2=(m2-4n2)2=m4-8m2n2+16n4;
⑧原式=a(-
a+
b+
c)=-
a2+
ab+
ac.
②原式=m2-9n2-m2+6mn-9n2=6mn-18n2;
③原式=(a-b)2-c2=a2-2ab+b2-c2;
④原式=x2-(2y-3)2=x2-4y2+12y-9;
⑤原式=(a-2b)2+2c(a-2b)+c2=a2-4ab+4b2+2ac-4bc+c2;
⑥原式=(x2-4xy+4y2-x2+4xy-4y2-4x2+2xy)÷2x=(-4x2+2xy)÷2x=-2x+y;
⑦原式=[(m+2n)(m-2n)]2=(m2-4n2)2=m4-8m2n2+16n4;
⑧原式=a(-
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 5 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 5 |
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若a2+2b2+5c2=4bc-2ab+2c-1,则a-b+c的值是( )
| A、-3 | B、0 | C、1 | D、2 |
下列计算正确的是( )
| A、xm+xm=x2m |
| B、2xn-xn=2 |
| C、x3•x3=2x3 |
| D、x2÷x6=x-4 |
 如图,P是直角三角形ABC的斜边BC上异于B、C的一点,过点P作直线截三角形ABC,使截得的三角形于三角形ABC相似,则过点P满足这样条件的直线最多有( )条.
如图,P是直角三角形ABC的斜边BC上异于B、C的一点,过点P作直线截三角形ABC,使截得的三角形于三角形ABC相似,则过点P满足这样条件的直线最多有( )条.
 如图,抛物线y=ax2+bx+2与x轴交于A、B两点,点A的坐标为(-1,0),抛物线的对称轴为直线x=1.5,点M为线段AB上一点,过M作x轴的垂线交抛物线于P,交过点A的直线y=-x+n于点C.
如图,抛物线y=ax2+bx+2与x轴交于A、B两点,点A的坐标为(-1,0),抛物线的对称轴为直线x=1.5,点M为线段AB上一点,过M作x轴的垂线交抛物线于P,交过点A的直线y=-x+n于点C.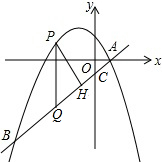 如图,在平面直角坐标系中,直线y=
如图,在平面直角坐标系中,直线y= 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作?A′PBE,A′E交射线BC于点F,交射线PQ于点G.设?A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作?A′PBE,A′E交射线BC于点F,交射线PQ于点G.设?A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.