题目内容
10．
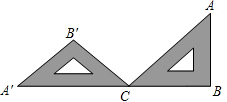如图，一块等腰直角的三角板ABC，在水平桌面上绕点C按逆时针方向旋转到A′B′C的位置，使A′、C、B三点共线，那么旋转角度的大小为135°．
分析 先利用等腰直角三角形的性质得∠ACB=45°，再根据旋转的性质得∠A′CA等于旋转角，然后利用邻补角计算∠A′CA的度数即可．
解答 解：∵△ABC为等腰直角三角形，
∴∠ACB=45°，
∵△ABC绕点C按逆时针方向旋转到△A′B′C的位置，使A′、C、B三点共线，
∴∠A′CA等于旋转角，
而∠A′CA=180°-∠ACB=180°-45°=135°，
∴旋转角度的大小为135°．
故答案为135°．
点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．下列计算正确的是（ ）
| A． | a2•a3=a5 | B． | a2+a3=a5 | C． | （a3）2=a5 | D． | a3÷a2=1 |
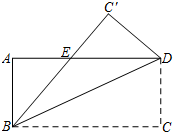如图，一张宽为3，长为4的长方形纸片ABCD，沿着对角线BD对折，点C落在点C′的位置，BC′交AD于E．
已知有理数a、b、c在数轴的对应位置如图，则|a-1|+|a-c|+|a-b|可化简为1-c-a+b．