题目内容
5.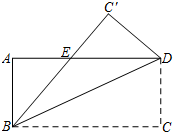 如图,一张宽为3,长为4的长方形纸片ABCD,沿着对角线BD对折,点C落在点C′的位置,BC′交AD于E.
如图,一张宽为3,长为4的长方形纸片ABCD,沿着对角线BD对折,点C落在点C′的位置,BC′交AD于E.(1)求证:BE=DE;
(2)求AE的长.
分析 (1)由折叠可知,∠CBD=∠EBD,再由AD∥BC,得到∠CBD=∠EDB,即可得到∠EBD=∠EDB,于是得到BE=DE;
(2)设AE=x,表示出BE,再利用勾股定理列出方程求解即可.
解答 解:(1)由折叠可知,∠CBD=∠EBD,
∵AD∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE;
(2)设AE=x,则BE=AD-AE=4-x,
在Rt△ABE中,AB2+AE2=BE2,
即32+x2=(4-x)2,
解得x=$\frac{7}{8}$,
即AE=$\frac{7}{8}$.
点评 本题主要考查翻折变换的知识点,解答本题的关键是熟练掌握等腰三角形的判定与勾股定理的知识,此题难度不大.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
8.方程x2+2x+3=$\frac{1}{x}$的实数根的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.(2a-5b)2=(2a+5b)2+N,则N的代数式是( )
| A. | -20ab | B. | 20ab | C. | 40ab | D. | -40ab |
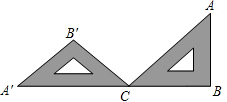 如图,一块等腰直角的三角板ABC,在水平桌面上绕点C按逆时针方向旋转到A′B′C的位置,使A′、C、B三点共线,那么旋转角度的大小为135°.
如图,一块等腰直角的三角板ABC,在水平桌面上绕点C按逆时针方向旋转到A′B′C的位置,使A′、C、B三点共线,那么旋转角度的大小为135°.