Question

1．如图，在边长为12的正方形ABCD中，边CD上有一动点E，将△ADE沿AE翻折得到△AEF，连接BD分别交AE，AF于点M，O，作∠BAF的角平分线AN交BD于点N，若BN=3$\sqrt{2}$，则OE=$\frac{6}{7}$$\sqrt{65}$．

Answer 1

分析 如图，将△ABN逆时针旋转90°得到△ADP，连接PM，作MG⊥AD于G，MH⊥AF于H，首先证明MN²=NB²+DM²，列出方程组求出MN、DM，再证明$\frac{AO}{AD}$=$\frac{OM}{DM}$，$\frac{AO}{AB}$=$\frac{ON}{BN}$，推出$\frac{OM}{DM}$=$\frac{ON}{BN}$，由此求出ON，求出OA、OF，根据$\frac{AG}{AD}$=$\frac{GM}{DE}$，求出DE，在Rt△OFE中利用勾股定理即可解决问题．

解答 解：如图，将△ABN逆时针旋转90°得到△ADP，连接PM，作MG⊥AD于G，MH⊥AF于H．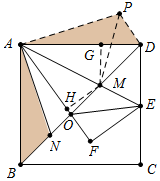

∵四边形ABCD是正方形，
∴AB=BC=CD=AD=12，
∴∠BAC=∠ADC=90°，
∵∠BAN=∠NAO，∠FAE=∠EAD，
∴∠NAM=45°，∠BAN+∠DAM=45°=∠DAM+∠DAP=∠MAP，
∴∠MAN=∠MAP，
在△MAN和△MAP中，
$\left\{\begin{array}{l}{MA=MA}\\{∠MAN=∠MAP}\\{AN=AP}\end{array}\right.$，
∴△MAN≌△MAP，
∴MN=MP，
∵∠ADP=∠ABN=∠ADM=45°，
∴∠MDP=90°，
∴PM²=PD²+DM²，
∵BN=PD，MN=PM，
∴MN²=BN²+DM²    ①
∴MN²=18+DM²，又∵BD=12$\sqrt{2}$，
∴MN+DM=9$\sqrt{2}$     ②
由①②得MN=5$\sqrt{2}$，DM=4$\sqrt{2}$，
∵∠MAO=∠MAD，MH⊥AO，MG⊥AD，
∴MH=MG，
∴$\frac{{S}_{△AOM}}{{S}_{△ADM}}$=$\frac{OM}{DM}$=$\frac{\frac{1}{2}•OA•MH}{\frac{1}{2}•AD•MG}$=$\frac{OA}{AD}$，
同理可得$\frac{OA}{AB}$=$\frac{ON}{BN}$，
∴$\frac{OM}{DM}$=$\frac{ON}{NB}$，
∴$\frac{OM}{ON}$=$\frac{DM}{BN}$=$\frac{4}{3}$，
∴ON=$\frac{15}{7}$$\sqrt{2}$，
∵$\frac{AB}{AO}$=$\frac{BN}{NO}$，
∴AO=$\frac{AB•ON}{BN}$=$\frac{60}{7}$，OF=AF-AO=12-$\frac{60}{7}$=$\frac{24}{7}$，
在Rt△DMG中，DM=4$\sqrt{2}$，∠MDG=45°，
∴GM=DG=4，
∴AG=8，
∵MG∥DE，
∴$\frac{AG}{AD}$=$\frac{GM}{DE}$，
∴$\frac{8}{12}$=$\frac{4}{DE}$，
∴DE=EF=6，
∴OE=$\sqrt{O{F}^{2}+E{F}^{2}}$=$\sqrt{（\frac{24}{7}）^{2}+{6}^{2}}$=$\frac{6}{7}$$\sqrt{65}$．
故答案为$\frac{6}{7}$$\sqrt{65}$．

点评 本题考查正方形的性质、翻折变换、全等三角形的判定和性质、平行线分线段成比例定理、角平分线的性质等知识，解题的关键是学会添加辅助线构造全等三角形，记住一些基本图形，基本结论，属于中考填空题中的压轴题．