题目内容
11. 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论::①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是①②.(请写出正确结论的序号).
如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论::①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是①②.(请写出正确结论的序号).
分析 利用SAS得到△EBF与△DFC全等,利用全等三角形对应边相等得到EF=AC,再由△ADC为等边三角形得到三边相等,等量代换得到EF=AD,AE=DF,利用对边相等的四边形为平行四边形得到AEFD为平行四边形,若AB=AC,∠BAC=120°,只能得到AEFD为菱形,不能为正方形,即可得到正确的选项.
解答 解:∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°,
∴∠ABE-∠ABF=∠FBC-∠ABF,即∠CBA=∠FBE,
在△ABC和△EBF中,
$\left\{\begin{array}{l}{AB=EB}\\{∠CBA=∠FBE}\\{BC=BF}\end{array}\right.$,
∴△ABC≌△EBF(SAS),
∴EF=AC,
又∵△ADC为等边三角形,
∴CD=AD=AC,
∴EF=AD=DC,
同理可得△ABC≌△DFC,
∴DF=AB=AE=DF,
∴四边形AEFD是平行四边形,选项②正确;
∴∠FEA=∠ADF,
∴∠FEA+∠AEB=∠ADF+∠ADC,即∠FEB=∠CDF,
在△FEB和△CDF中,
$\left\{\begin{array}{l}{EF=DC}\\{∠FEB=∠CDF}\\{EB=FD}\end{array}\right.$.
∴△FEB≌△CDF(SAS),选项①正确;
若AB=AC,∠BAC=120°,则有AE=AD,∠EAD=120°,此时AEFD为菱形,选项③错误,
故答案为:①②.
点评 本题考查了全等三角形的判定与性质,等边三角形的性质,平行四边形的判定,以及正方形的判定,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
16.计算12+(-18)÷(-6)-(-3)×2的结果是( )
| A. | 7 | B. | 8 | C. | 21 | D. | 36 |
3.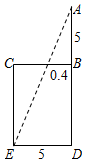 “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
 “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )| A. | 1.25尺 | B. | 57.5尺 | C. | 6.25尺 | D. | 56.5尺 |
20.把0.0813写成a×10n(1≤a<10,n为整数)的形式,则a为( )
| A. | 1 | B. | -2 | C. | 0.813 | D. | 8.13 |
1.用科学记数法表示136 000,其结果是( )
| A. | 0.136×106 | B. | 1.36×105 | C. | 136×103 | D. | 136×106 |
 有一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:AC平分∠BAD.
有一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:AC平分∠BAD.