题目内容
19.(1)计算:(-1)5+15×3-2-$\frac{{\sqrt{12}×\sqrt{2}}}{{\sqrt{6}}}$;(2)求不等式组:$\left\{\begin{array}{l}1-3x<6\\ \frac{x+1}{2}>x-1\end{array}$的所有整数解.
分析 先求出每个不等式的解集,在数轴上表示不等式的解集,再求出不等式组的解集即可.
解答 解:(1)原式=-1+15×$\frac{1}{9}$-$\frac{{\sqrt{6}×\sqrt{2}×\sqrt{2}}}{{\sqrt{6}}}$
=-1+$\frac{5}{3}$-2
=-$\frac{4}{3}$;
(2)$\left\{\begin{array}{l}{1-3x<6①}\\{\frac{x+1}{2}>x-1②}\end{array}\right.$
∵解不等式①得x>-$\frac{5}{3}$,
解不等式②得x<2,
∴不等式组的解集为-$\frac{5}{3}$<x<2,
∴不等式组的所有整数解为-1,0,1.
点评 本题考查了有理数的乘方,负整数指数幂,二次根式的性质,解一元一次不等式和解一元一次不等式组等知识点,能灵活运用知识点进行计算是解此题的关键.

练习册系列答案
相关题目
10.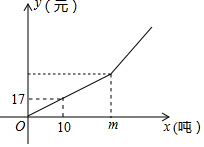 为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费$\frac{m}{100}$元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:
为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费$\frac{m}{100}$元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:
(1)求出m的值;
(2)写出y与x之间的函数关系式,并指出自变量x的取值范围.
 为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费$\frac{m}{100}$元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:
为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费$\frac{m}{100}$元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:| 月份 | 用水量x(吨) | 水费y(元) |
| 四月 | 35 | 59.5 |
| 五月 | 80 | 151 |
(2)写出y与x之间的函数关系式,并指出自变量x的取值范围.
8.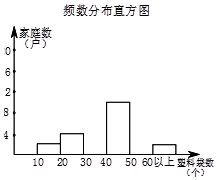 小明要统计小区500户居民每月丢弃塑料袋的数量情况,他随机调查了其中40户居民,按每月丢弃的塑料袋的数量分组进行统计,并绘制了如下的频数分布表和频数分布直方图:
小明要统计小区500户居民每月丢弃塑料袋的数量情况,他随机调查了其中40户居民,按每月丢弃的塑料袋的数量分组进行统计,并绘制了如下的频数分布表和频数分布直方图:
根据以上提供的信息,解答下列问题:
(1)补全频数分布表和频数分布直方图;
(2)请你估算该小区每月丢弃塑料袋的数不少于40个的户数大约有多少户?
 小明要统计小区500户居民每月丢弃塑料袋的数量情况,他随机调查了其中40户居民,按每月丢弃的塑料袋的数量分组进行统计,并绘制了如下的频数分布表和频数分布直方图:
小明要统计小区500户居民每月丢弃塑料袋的数量情况,他随机调查了其中40户居民,按每月丢弃的塑料袋的数量分组进行统计,并绘制了如下的频数分布表和频数分布直方图:| 组别 | 每月丢塑料袋个数 | 频数 | 频率 |
| 第1组 | 10至19 | 2 | 0.05 |
| 第2组 | 20至29 | 4 | 0.10 |
| 第3组 | 30至39 | 6 | 0.15 |
| 第4组 | 40至49 | 10 | 0.25 |
| 第5组 | 50至59 | 16 | 0.40 |
| 第6组 | 60以上 | 2 | 0.05 |
| 合计 | 40 | 1.00 |
(1)补全频数分布表和频数分布直方图;
(2)请你估算该小区每月丢弃塑料袋的数不少于40个的户数大约有多少户?
9. 如图是一个空心圆柱体,它的左视图是( )
如图是一个空心圆柱体,它的左视图是( )
 如图是一个空心圆柱体,它的左视图是( )
如图是一个空心圆柱体,它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论::①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是①②.(请写出正确结论的序号).
如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论::①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是①②.(请写出正确结论的序号).