题目内容
若一个多边形的内角和比四边形的内角和多1080°，并且这个多边形的各内角都相等．这个多边形的每个内角等于多少度？
考点：多边形内角与外角
专题：
分析：本题首先由题意得出等量关系，即这个多边形的内角和比四边形的内角和多540°，由此列出方程解出边数，进一步可求出它每一个内角的度数．
解答：解：设这个多边形的边数为n，
则有（n-2）•180°=360°+1080°，
解得n=10．
∵这个多边形的每个内角都相等，
∴它每一个内角的度数为1440°÷10=144°，
答：这个多边形的每个内角等于144度．
则有（n-2）•180°=360°+1080°，
解得n=10．
∵这个多边形的每个内角都相等，
∴它每一个内角的度数为1440°÷10=144°，
答：这个多边形的每个内角等于144度．
点评：本题主要考查多边形的内角和定理，解题的根据是已知等量关系列出方程从而解决问题．
练习册系列答案
全优点练单元计划系列答案
相关题目
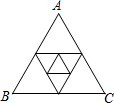如图，△ABC的三边长分别为a，b，c，以它的三边中点为顶点组成一个新三角形，以这个新三角形三边中点为顶点又组成一个小三角形，求这个小三角形的周长．
如图，写出八边形其余各顶点坐标．