题目内容
16. 已知:如图,菱形ABCD 中,过AD 的中点 E作AC 的垂线EF,交AB 于点 M,交CB 的延长线于点F.如果FB的长是 $\sqrt{2}$,∠AEM=30°.求菱形ABCD 的周长和面积.
已知:如图,菱形ABCD 中,过AD 的中点 E作AC 的垂线EF,交AB 于点 M,交CB 的延长线于点F.如果FB的长是 $\sqrt{2}$,∠AEM=30°.求菱形ABCD 的周长和面积.
分析 首先连接BD,易证得四边形EFBD为平行四边形,即可求得AD的长,继而求得菱形ABCD的周长,求出对角线的长度,利用菱形的面积=对角线乘积的一半求出面积.
解答 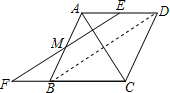 解:连接BD.
解:连接BD.
∵在菱形ABCD中,
∴AD∥BC,AC⊥BD.
又∵EF⊥AC,
∴BD∥EF.
∴四边形EFBD为平行四边形.
∴FB=ED=$\sqrt{2}$.
∵∠AEM=30°
∴BD=2$\sqrt{6}$,AC=2$\sqrt{2}$,
∵E是AD的中点.
∴AD=2ED=2$\sqrt{2}$.
∴菱形ABCD的周长为4×2$\sqrt{2}$=8$\sqrt{2}$,
∴菱形ABCD的面积为$\frac{1}{2}$×2$\sqrt{6}$×2$\sqrt{2}$=4$\sqrt{3}$.
点评 本题考查了菱形的性质,主要利用了菱形的对角线互相垂直的性质,菱形的四条边都相等的性质,掌握菱形的面积=对角线乘积的一半求出面积.

练习册系列答案
相关题目
4.下列计算中,正确的是 ( )
| A. | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B. | $2+\sqrt{3}=2\sqrt{3}$ | C. | $\sqrt{8}×\sqrt{2}=4$ | D. | $\frac{{\sqrt{10}}}{2}=\sqrt{5}$ |
11.不等式2x≤6的在数轴上表示为( )
| A. |  | B. |  | ||
| C. |  | D. |  |
 如图,双曲线$y=\frac{3}{x}(x>0)$经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB'C,B'点落在OA上,则四边形OABC的面积是3.
如图,双曲线$y=\frac{3}{x}(x>0)$经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB'C,B'点落在OA上,则四边形OABC的面积是3. 如图,在菱形ABCD中,已知∠DAB=60°,AB=2,求AC的长和菱形的面积.
如图,在菱形ABCD中,已知∠DAB=60°,AB=2,求AC的长和菱形的面积.
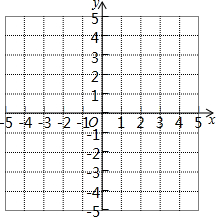 在平面直角坐标系中,点O为坐标原点,已知点A(2,0)和点B(2,2),请画出△OAB以及一个以点O为位似中心的△OAB的位似图形△OA'B',使△OAB与△OA'B'的相似比为1:2.
在平面直角坐标系中,点O为坐标原点,已知点A(2,0)和点B(2,2),请画出△OAB以及一个以点O为位似中心的△OAB的位似图形△OA'B',使△OAB与△OA'B'的相似比为1:2.
 如图,∠1、∠2是△ABC的外角,已知∠1+∠2=260°,求∠A的度数是80°.
如图,∠1、∠2是△ABC的外角,已知∠1+∠2=260°,求∠A的度数是80°.