题目内容
 如图,在半径为
如图,在半径为 ,圆心角等于45°的扇形AOB内部作一个矩形CDEF,使点C在OA上,点D、E在OB上,点F在弧AB上,且DE=2CD,则:
,圆心角等于45°的扇形AOB内部作一个矩形CDEF,使点C在OA上,点D、E在OB上,点F在弧AB上,且DE=2CD,则:(1)弧AB的长是(结果保留π) ;
(2)图中阴影部分的面积为(结果保留π) .
【答案】分析:(1)根据弧长公式l= ,计算即可;
,计算即可;
(2)用扇形的面积减去三角形的OCD和矩形CDFE面积即可.连接OF,利用勾股定理求出OD的长.
解答:解:(1)∵n=45°,r= ,
,
∴l= =
= =
= ;
;
 (2)连接OF,设CD=x,则DE=2x
(2)连接OF,设CD=x,则DE=2x
∵∠O=45°,则OD=x,
在直角三角形OEF中,由勾股定理得OE2+EF2=OF2,
即(3x)2+x2= ,
,
解得x=±1(舍去负数),
∴OD=1,
S阴影=S扇形AOB-S△OCD-S矩形CDFE
= -
- -1×2,
-1×2,
= -
- ,
,
= .
.
故答案为: ;
; .
.
点评:本题考查了扇形面积的计算,弧长的计算,熟练掌握弧长公式l= ,是解题的关键.
,是解题的关键.
 ,计算即可;
,计算即可;(2)用扇形的面积减去三角形的OCD和矩形CDFE面积即可.连接OF,利用勾股定理求出OD的长.
解答:解:(1)∵n=45°,r=
 ,
,∴l=
 =
= =
= ;
; (2)连接OF,设CD=x,则DE=2x
(2)连接OF,设CD=x,则DE=2x∵∠O=45°,则OD=x,
在直角三角形OEF中,由勾股定理得OE2+EF2=OF2,
即(3x)2+x2=
 ,
,解得x=±1(舍去负数),
∴OD=1,
S阴影=S扇形AOB-S△OCD-S矩形CDFE
=
 -
- -1×2,
-1×2,=
 -
- ,
,=
 .
.故答案为:
 ;
; .
.点评:本题考查了扇形面积的计算,弧长的计算,熟练掌握弧长公式l=
 ,是解题的关键.
,是解题的关键. 
练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
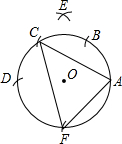 如图,在半径为1的⊙O上任取一点A,连续以1为半径在⊙O上截取AB=BC=CD,分别以A、D为圆心A到C的距离为半径画弧,两弧交于E,以A为圆心O到E的距离为半径画弧,交⊙O于F.则△ACF面积是( )
如图,在半径为1的⊙O上任取一点A,连续以1为半径在⊙O上截取AB=BC=CD,分别以A、D为圆心A到C的距离为半径画弧,两弧交于E,以A为圆心O到E的距离为半径画弧,交⊙O于F.则△ACF面积是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,在半径为5的⊙O中,弦AB=8,圆心O到弦AB的距离等于( )
如图,在半径为5的⊙O中,弦AB=8,圆心O到弦AB的距离等于( )| A、5 | B、4 | C、3 | D、6 |
 如图,在半径为5cm的⊙O中,圆心O到弦AB的距离为3cm,则弦AB的长是( )
如图,在半径为5cm的⊙O中,圆心O到弦AB的距离为3cm,则弦AB的长是( ) 如图,在半径为5的⊙O中,点A、B在⊙O中,∠AOB=90°,点C是
如图,在半径为5的⊙O中,点A、B在⊙O中,∠AOB=90°,点C是
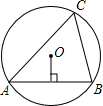 如图,在半径为2的⊙O中,圆心0到弦AB的距离为1,C为AB上方圆弧上任意一点,则∠ACB=
如图,在半径为2的⊙O中,圆心0到弦AB的距离为1,C为AB上方圆弧上任意一点,则∠ACB=