题目内容
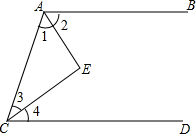 如图,AB∥CD,∠BAC和∠ACD的平分线相交于点E,求证:AE⊥CE.
如图,AB∥CD,∠BAC和∠ACD的平分线相交于点E,求证:AE⊥CE.证明:∵AE平分∠BAC(
∴∠1=∠2(
∵CE平分∠ACD,∴∠3=∠4
∵AB∥CD,
∴∠BAC+∠AC=
∴∠1+∠2+∠3+∠4=
∴∠1+∠3=
∴∠E=180°-(∠1+∠3)=
∴AE⊥CE(
考点:平行线的性质,垂线
专题:证明题
分析:根据平行线的性质和角平分线的定义可求得∠1+∠3=90°,从而可证得AE⊥CE.依据此过程填空即可.
解答:证明:∵AE平分∠BAC( 已知)
∴∠1=∠2( 角平分线的定义)
∵CE平分∠ACD,∴∠3=∠4
∵AB∥CD,
∴∠BAC+∠AC=180°( 两直线平行,同旁内角互补)
∴∠1+∠2+∠3+∠4=180°
∴∠1+∠3=90°
∴∠E=180°-(∠1+∠3)=90°
∴AE⊥CE( 垂直的定义)
故答案为:已知;角平分线的定义;180°;两直线平行,同旁内角互补;180°;90°;90°;垂直的定义.
∴∠1=∠2( 角平分线的定义)
∵CE平分∠ACD,∴∠3=∠4
∵AB∥CD,
∴∠BAC+∠AC=180°( 两直线平行,同旁内角互补)
∴∠1+∠2+∠3+∠4=180°
∴∠1+∠3=90°
∴∠E=180°-(∠1+∠3)=90°
∴AE⊥CE( 垂直的定义)
故答案为:已知;角平分线的定义;180°;两直线平行,同旁内角互补;180°;90°;90°;垂直的定义.
点评:本题主要考查平行线的性质,掌握平行线的性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一双运动鞋先按成本提高40%标价,再以8折(标价的80%)出售,结果获利27元,若设这双运动鞋的成本价是x元,根据题意,可得到的方程是( )
| A、(1+40%)x•80%=x-27 |
| B、(1+40%)x•80%=x+27 |
| C、(1-40%)x•80%=x+27 |
| D、(1-40%)x•80%=x+27 |
下列事件中,必然事件是( )
| A、抛掷1个均匀的骰子,出现6点向上 |
| B、两直线被第三条直线所截,同位角相等 |
| C、366人中至少有2人的生日相同 |
| D、实数的绝对值是非负数 |
