题目内容
2．已知等腰三角形的周长是18cm，腰长y（cm）是底边长x（cm）的函数，试求函数的关系式，并写出自变量的取值范围．分析 根据已知列出方程，再根据三角形三边的关系明确定义域即可．
解答 解：∵2y+x=18，
∴y=9-$\frac{1}{2}$x，即x＜10，
根据三角形的三边关系得：
$\left\{\begin{array}{l}{x+x＞9-\frac{1}{2}x}\\{-\frac{1}{2}x+9＞0}\end{array}\right.$，
解得：$\frac{18}{5}$＜x＜18．
所以取值范围为：0＜x＜9．
点评 本题考查了一次函数的问题，关键是根据等腰三角形三边关系的性质，三角形三边关系定理分析．
练习册系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
在△ABC中，D，E，F分别是三边上的点，且∠1=∠2，∠C=∠EDF，试求证：DF∥CA，DE∥BC．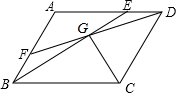
已知：在?ABCD中，E为AD上一点，F为AB上一点，且BE=DF，BE与DF交于G．
11．
如图所示，在菱形ABCD中E是AB的中点，作EF∥BC，交AC于点F，EF=4，那么菱形的周长为（ ）
如图所示，在菱形ABCD中E是AB的中点，作EF∥BC，交AC于点F，EF=4，那么菱形的周长为（ ）| A． | 16 | B． | 30 | C． | 28 | D． | 32 |
