题目内容
15.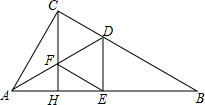 如图,△ABC中,∠ACB=90°,AD是∠CAB的平分线,交BC于D,CH是AB边上的高,交AD于F,DE⊥AB于E,求证:四边形CDEF是菱形.
如图,△ABC中,∠ACB=90°,AD是∠CAB的平分线,交BC于D,CH是AB边上的高,交AD于F,DE⊥AB于E,求证:四边形CDEF是菱形.
分析 由角平分线的定义得出DC=DE,由垂线的性质得出CH∥DE,由角的互余关系和对顶角相等得出∠CDF=∠CFD,得出CF=DC,因此CF=DE,得出四边形CDEF是平行四边形,即可得出结论.
解答 证明:∵∠ACB=90°,AD是∠CAB的平分线,DE⊥AB,
∴DC=DE,∠CAD=∠EAD,∠CDF+∠CAD=90°,
∵CH是AB边上的高,
∴CH⊥AB,
∴CH∥DE,∠AFH+∠EAD=90°,
∴∠CDF=∠AFH,
∵∠CFD=∠AFH,
∴∠CDF=∠CFD,
∴CF=DC,
∴CF=DE,
∴四边形CDEF是平行四边形,
∴四边形CDEF是菱形.
点评 本题考查了角平分线的性质、等腰三角形的判定、对顶角相等、平行四边形的判定、菱形的判定等知识;本题综合性强,有一定难度,证明四边形是平行四边形是解决问题的关键.

练习册系列答案
相关题目
3.两个数相加,如果和小于每个加数,那么( )
| A. | 这两个加数同为正数 | B. | 这两个加数的符号不同 | ||
| C. | 这两个加数同为负数 | D. | 这两个加数中有一个为零 |
7.下列几个命题:①圆中最长的弦是直径;②经过半径的外端,且垂直于这条半径的直线是圆的切线;③相等的圆心角所对的弧相等;④等弧所对的圆周角相等,且等于该弧所对圆心角的一半;⑤三角形的内心是三边垂直平分线的交点,它到三角形三顶点的距离相等. 其中真命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.若x是不等于1的实数,我们把$\frac{1}{1-x}$称为x的差倒数,如2的差倒数是$\frac{1}{1-2}$=-1,-1的差倒数为$\frac{1}{1-(-1)}$=$\frac{1}{2}$.现已知x1=-$\frac{1}{3}$,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差倒数,…,依此类推,则x2015的值为( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | 4 |