题目内容
4.若x是不等于1的实数,我们把$\frac{1}{1-x}$称为x的差倒数,如2的差倒数是$\frac{1}{1-2}$=-1,-1的差倒数为$\frac{1}{1-(-1)}$=$\frac{1}{2}$.现已知x1=-$\frac{1}{3}$,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差倒数,…,依此类推,则x2015的值为( )| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | 4 |
分析 根据差倒数的定义分别计算出x1=-$\frac{1}{3}$,x2=$\frac{3}{4}$;x3=4,x4=-$\frac{1}{3}$,…得到从x1开始每3个值就循环,而2015÷3=671…2,即可得出答案.
解答 解:∵x1=-$\frac{1}{3}$,
∴x2=$\frac{1}{1-(-\frac{1}{3})}$=$\frac{3}{4}$;
x3=$\frac{1}{1-\frac{3}{4}}$=4;
x4=$\frac{1}{1-4}$=-$\frac{1}{3}$;
…,
∴三个数一个循环,
∵2015÷3=671…2,
∴x2015=x2=$\frac{3}{4}$.
故选:C.
点评 此题考查了数字的变化规律,通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
14.如果分式$\frac{x-2}{x}$的值为0,那么x的值为( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
12.如果有理数x的相反数是3,并且|y|=5,那么x+y=( )
| A. | -8 | B. | 2 | C. | 8或-2 | D. | -8或2 |
14.(1)填表:
(2)由上你发现了什么规律?用语言叙述这个规律.
| a | 0.0001 | 0.01 | 1 | 100 | 10000 |
| $\sqrt{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
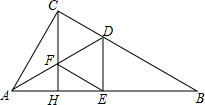 如图,△ABC中,∠ACB=90°,AD是∠CAB的平分线,交BC于D,CH是AB边上的高,交AD于F,DE⊥AB于E,求证:四边形CDEF是菱形.
如图,△ABC中,∠ACB=90°,AD是∠CAB的平分线,交BC于D,CH是AB边上的高,交AD于F,DE⊥AB于E,求证:四边形CDEF是菱形. 桌上摆着一个由若干个相同的正方体组成的几何体,其主视图和左视图如图所示,这个几何体最多可以由27个这样的正方体组成.最少可以由15个这样的正方体组成.
桌上摆着一个由若干个相同的正方体组成的几何体,其主视图和左视图如图所示,这个几何体最多可以由27个这样的正方体组成.最少可以由15个这样的正方体组成.