题目内容
 已知:抛物线y=ax2+bx+c(a≠0)在平面直角坐标系的位置如图所示,则下列结论中正确的是( )
已知:抛物线y=ax2+bx+c(a≠0)在平面直角坐标系的位置如图所示,则下列结论中正确的是( )| A、abc>0 |
| B、4a-b=0 |
| C、9a+3b+c<0 |
| D、5a+c>0 |
考点:二次函数图象与系数的关系
专题:压轴题,数形结合
分析:由抛物线开口向下得a<0;由抛物线的对称轴为直线x=-
=2得到b>0;由抛物线与y轴的交点坐标在x轴上方得到c>0,则可对A、B进行判断;根据抛物线的对称性可得到x=3时,y>0,即9a+3b+c>0,可对C进行判断;由x=-1时,y>0,即a-b+c=0,然后把b=-4a代入,则可对D进行判断.
| b |
| 2a |
解答:解:A、∵抛物线开口向下,∴a<0;∵抛物线的对称轴为直线x=-
=2,∴b>0;∵抛物线与y轴的交点坐标在x轴上方,∴c>0,∴abc<0,所以A选项错误;
B、∵抛物线的对称轴为直线x=-
=2,∴4a-b=0,所以B选项错误;
C、∵抛物线与x轴的一个交点的横坐标在-2与-1之间,而抛物线的对称轴为x=2,∴x=3时,y>0,9a+3b+c>0,所以C选项错误;
D、∵x=-1时,y>0,∴a-b+c=0,∵b=-4a,∴5a+c>0,所以D选项正确.
故选D.
| b |
| 2a |
B、∵抛物线的对称轴为直线x=-
| b |
| 2a |
C、∵抛物线与x轴的一个交点的横坐标在-2与-1之间,而抛物线的对称轴为x=2,∴x=3时,y>0,9a+3b+c>0,所以C选项错误;
D、∵x=-1时,y>0,∴a-b+c=0,∵b=-4a,∴5a+c>0,所以D选项正确.
故选D.
点评:本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-
;抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点.
| b |
| 2a |

练习册系列答案
相关题目
分式
有意义的条件是( )
| x |
| x-1 |
| A、x≠0 | B、x≠1 |
| C、x≥0 | D、x>1 |
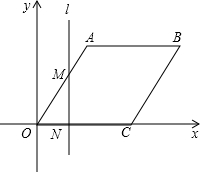 如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).
如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).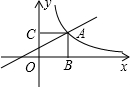 如图,直线y=kx+1与反比例函数
如图,直线y=kx+1与反比例函数