题目内容
10．二次函数y=ax2+k（a≠0）的图象经过点A（1，-1），B（2，5）．（1）求该函数的解析式．
（2）若点C（-2，m），D（n，7）也在函数的图象上，求m，n的值．
分析 （1）直接把两个已知点的坐标代入y=ax2+k（a≠0）得到关于a、k的方程组，然后解关于a和k的方程组求出a和k的值即可．
（2）把点C（-2，m），D（n，7）代入（1）中的解析式可求得结果．
解答 解：（1）根据题意得，
$\left\{\begin{array}{l}{a+k=-1}\\{\;}\\{4a+k=5}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=2}\\{\;}\\{k=-3}\end{array}\right.$，
所以二次函数解析式为y=2x2-3；
（2）∵点C（-2，m）在函数的图象上，
∴m=2×（-2）2-3=5；
∵点D（n，7）在函数的图象上，
∴7=2n2-3
解得，n=$±\sqrt{5}$．
点评 本题考查了待定系数法求二次函数的解析式，利用代入法是解答此题的关键．
练习册系列答案
相关题目
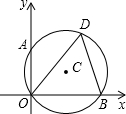如图，⊙C经过原点且与两坐标轴分别交于点A和点B，点A的坐标为（0，2），D为⊙C在第一象限内的一点且∠ODB=60°，解答下列各题：
分别画如图几何体的主视图、左视图、俯视图．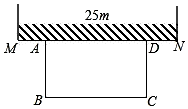
如图，某农场老板准备建造一个矩形羊圈ABCD，他打算让矩形羊圈的一面完全靠着墙MN，墙MN可利用的长度为25m，另外三面用长度为50m的篱笆围成（篱笆正好要全部用完，且不考虑接头的部分），设矩形羊圈的面积为ym2，垂直于墙的一边长AB为x m．
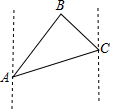如图，一艘油轮在海中航行，在A点看到小岛B在A的北偏东25°方向距离60海里处，油轮沿北偏东70°方向航行到C处，看到小岛B在C的北偏西50°方向，则油轮从A航行到C处的距离是（ ）海里．（结果保留整数）（参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.74，$\sqrt{6}$≈2.45）