题目内容
20. 如图,一个圆柱的高为10cm,底面周长为24cm,动点P从A点出发,沿着圆柱侧面移动到BC的中点S,求移动的最短距离.
如图,一个圆柱的高为10cm,底面周长为24cm,动点P从A点出发,沿着圆柱侧面移动到BC的中点S,求移动的最短距离.
分析 由于圆柱的高为10cm,S为BC的中点,故BS=5cm,先把圆柱的侧面展开,连接AS,利用勾股定理即可得出AS的长.
解答  解:沿着S所在的母线展开,如图
解:沿着S所在的母线展开,如图
连接AS,则AB=$\frac{1}{2}$×24=12,BS=$\frac{1}{2}$BC=5,
在Rt△ABS中,根据勾股定理
AB2+BS2=AS2,即122+52=AS2,
解得AS=13.
∵A,S两点之间线段AS最短,
∴点A到点S移动的最短距离为AS=13cm.
点评 本题考查的是平面展开-最短路径问题,根据题意画出圆柱的侧面展开图,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
10.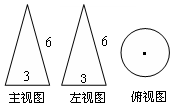 一个几何体的三视图如图,其中主视图都是腰长为6、底边长为3的等腰三角形,则这个几何体的侧面展开图的面积为( )
一个几何体的三视图如图,其中主视图都是腰长为6、底边长为3的等腰三角形,则这个几何体的侧面展开图的面积为( )
 一个几何体的三视图如图,其中主视图都是腰长为6、底边长为3的等腰三角形,则这个几何体的侧面展开图的面积为( )
一个几何体的三视图如图,其中主视图都是腰长为6、底边长为3的等腰三角形,则这个几何体的侧面展开图的面积为( )| A. | 3π | B. | 18π | C. | 8π | D. | 9π |
 如图,已知HM平分∠EHD,GB∥HD,∠3=35°.
如图,已知HM平分∠EHD,GB∥HD,∠3=35°.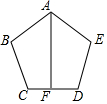 如图,已知AB=AE,∠ABC=∠AED,BC=ED,点F是CD的中点,连接A,F.AF与CD有怎样的关系?并说明理由.
如图,已知AB=AE,∠ABC=∠AED,BC=ED,点F是CD的中点,连接A,F.AF与CD有怎样的关系?并说明理由. 如图,数轴上的点P表示的数是-1,将点P向左平移1个单位长度再向右平移9个单位长度后得到点P′,则点P平移经过了8个非负整数点.
如图,数轴上的点P表示的数是-1,将点P向左平移1个单位长度再向右平移9个单位长度后得到点P′,则点P平移经过了8个非负整数点.