题目内容
17.在△ABC中,∠C=90°,BC=3,AC=4,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
分析 根据题意画出图形,由勾股定理求出AB的长,再根据三角函数的定义解答即可.
解答  解:在△ABC中,∠C=90°,
解:在△ABC中,∠C=90°,
∵AC=4,BC=3,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5.
∴sinA=$\frac{3}{5}$,
故选:B.
点评 本题考查锐角三角函数的定义:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
相关题目
7.一个底面直径为2,高为3的圆锥的体积是( )
| A. | π | B. | 2π | C. | 3π | D. | 4π |
12. 如图,数轴上的四个点A、B、C、D位置如图所示,它们分别对应四个实数a、b、c、d,若a+c=0,AB<BC,则下列各式正确的是( )
如图,数轴上的四个点A、B、C、D位置如图所示,它们分别对应四个实数a、b、c、d,若a+c=0,AB<BC,则下列各式正确的是( )
 如图,数轴上的四个点A、B、C、D位置如图所示,它们分别对应四个实数a、b、c、d,若a+c=0,AB<BC,则下列各式正确的是( )
如图,数轴上的四个点A、B、C、D位置如图所示,它们分别对应四个实数a、b、c、d,若a+c=0,AB<BC,则下列各式正确的是( )| A. | bc>0 | B. | b-d>0 | C. | b+c>0 | D. | |a|>|d| |
6.不等式5x>4x+2的解集在数轴上表示正确的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
7.下列各组数中,把两数相乘,积为1的是( )
| A. | 2和-2 | B. | -2和$\frac{1}{2}$ | C. | $\sqrt{3}$和$\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$和-$\sqrt{3}$ |
 如图,AB是⊙O的直径,CD为⊙O的弦,过点B作⊙O的切线,交AD的延长线于点E,连接AC并延长,过点E作EG⊥AC的延长线于点G,并且∠GCD=∠GAB.
如图,AB是⊙O的直径,CD为⊙O的弦,过点B作⊙O的切线,交AD的延长线于点E,连接AC并延长,过点E作EG⊥AC的延长线于点G,并且∠GCD=∠GAB.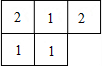 由7个相同的小正方体搭成一个几何体,其俯视图如图所示,其中小正方形中数字表示该位置小正方体的个数,则该几何体的左视图是( )
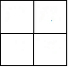
由7个相同的小正方体搭成一个几何体,其俯视图如图所示,其中小正方形中数字表示该位置小正方体的个数,则该几何体的左视图是( )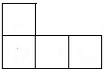


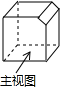 如图,是一个正方体被切掉一条棱后所得的几何体,则它的左视图是( )
如图,是一个正方体被切掉一条棱后所得的几何体,则它的左视图是( )