题目内容
已知在平行四边形ABCD中,对角线BD=14,过平行四边形ABCD的顶点D作高,垂足为H,连接OH,则OH= .
【答案】分析:由四边形ABCD是平行四边形,可得OB=OD,又由DH⊥BH,根据直角三角形斜边上的中线等于斜边的一半,即可求得答案.
解答:解:∵四边形ABCD是平行四边形,
∴OB=OD,
∵DH⊥BH,
∴∠BHD=90°,
在Rt△BHD中,OH= BD=
BD= ×14=7.
×14=7.
故答案为:7.
点评:此题考查了平行四边形的性质以及直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.
解答:解:∵四边形ABCD是平行四边形,
∴OB=OD,
∵DH⊥BH,
∴∠BHD=90°,
在Rt△BHD中,OH=
 BD=
BD= ×14=7.
×14=7.故答案为:7.
点评:此题考查了平行四边形的性质以及直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
已知在平行四边形ABCD中,向量
=
,
=
,那么向量
等于( )
| AB |
| a |
| BC |
| b |
| BD |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
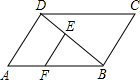 如图,已知在平行四边形ABCD中,点E、F分别在线段 BD、AB上,EF∥AD,DE:EB=2:3,EF=9,那么BC的长为
如图,已知在平行四边形ABCD中,点E、F分别在线段 BD、AB上,EF∥AD,DE:EB=2:3,EF=9,那么BC的长为 如图,已知在平行四边形ABCD中,DE:EC=2:3,
如图,已知在平行四边形ABCD中,DE:EC=2:3, 18、已知在平行四边形ABCD中,DE⊥AB,DF⊥BC,∠EDF=135°,求平行四边形各角的度数.
18、已知在平行四边形ABCD中,DE⊥AB,DF⊥BC,∠EDF=135°,求平行四边形各角的度数.