题目内容
 18、已知在平行四边形ABCD中,DE⊥AB,DF⊥BC,∠EDF=135°,求平行四边形各角的度数.
18、已知在平行四边形ABCD中,DE⊥AB,DF⊥BC,∠EDF=135°,求平行四边形各角的度数.分析:可先由垂直关系得出∠ADE=∠CDF,进而依据∠ADE与∠ADC的度数关系进行求解,即可得出结论.
解答:解:∵DE⊥AB,∠EDF=135°,
∴∠CDF=45°,
在平行四边形ABCD中,DF⊥BC,
则∠B=∠DCF=90°-45°=45°,
则∠BAD=135°.
∴平行四边形各角的度数为:135°,45°,135°,45°.
∴∠CDF=45°,
在平行四边形ABCD中,DF⊥BC,
则∠B=∠DCF=90°-45°=45°,
则∠BAD=135°.
∴平行四边形各角的度数为:135°,45°,135°,45°.
点评:本题主要考查了平行四边形的性质问题,能够运用平行四边形的性质进行一些简单的计算问题.

练习册系列答案
相关题目
已知在平行四边形ABCD中,向量
=
,
=
,那么向量
等于( )
| AB |
| a |
| BC |
| b |
| BD |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
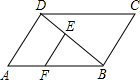 如图,已知在平行四边形ABCD中,点E、F分别在线段 BD、AB上,EF∥AD,DE:EB=2:3,EF=9,那么BC的长为
如图,已知在平行四边形ABCD中,点E、F分别在线段 BD、AB上,EF∥AD,DE:EB=2:3,EF=9,那么BC的长为 如图,已知在平行四边形ABCD中,DE:EC=2:3,
如图,已知在平行四边形ABCD中,DE:EC=2:3,