题目内容
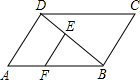如图，已知在平行四边形ABCD中，点E、F分别在线段 BD、AB上，EF∥AD，DE：EB=2：3，EF=9，那么BC的长为分析：先利用DE：EB=2：3，求得
=
，再利用平行四边形，证明△EFB∽△ADB，再利用对应边成比例即可解题．
| EB |
| BD |
| 3 |
| 5 |
解答：解：由
=
，得
=
即
=
，
∵EF∥AD，
∴△EFB∽△ADB，
∴
=
，
∴
=
，
解得AD=15，
因在平行四边形ABCD中，
所以AD=BC=15．
故答案为：15．
| DE |
| EB |
| 2 |
| 3 |
| DE+EB |
| EB |
| 5 |
| 3 |
| EB |
| BD |
| 3 |
| 5 |
∵EF∥AD，
∴△EFB∽△ADB，
∴
| EB |
| DB |
| EF |
| AD |
∴
| 9 |
| AD |
| 3 |
| 5 |
解得AD=15，
因在平行四边形ABCD中，
所以AD=BC=15．
故答案为：15．
点评：此题主要考查学生利用平行四边形的性质证明三角形相似，从而利用相似三角形的对应边成比例来解题的．
练习册系列答案
相关题目
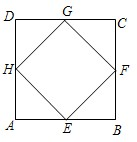四个顶点都在正方形边上的四边形叫做正方形的内接四边形．如图，四边形EFGH是正方形ABCD的内接平行四边形，且已知正方形ABCD的边长为4．
，BO＝AO．又∵AG⊥EB，∠1＋∠3＝
＝∠2＋∠3∴∠1＝∠2，∴Rt△BOE≌Rt△AOF解答此题后某同学产生了如下猜想：对上述命题，若点E在AC的延长线上，AG⊥EB，AG交EB的延长线于G，AG的延长线交DB的延长线于F，其它条件不变，如图，则仍有OE＝OF．问猜想所得的结论是否成立，请说明理由．
