题目内容
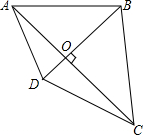 如图,在四边形ABCD中,AC和BD相交于点O,且∠AOD=90°.
如图,在四边形ABCD中,AC和BD相交于点O,且∠AOD=90°.(1)求证:AD2+BC2=AB2+CD2;
(2)若BC=2AD,AB=12,CD=9,求四边形ABCD的周长.
考点:勾股定理
专题:
分析:(1)利用勾股定理可得AO2+DO2=AD2,BC2=BO2+OC2,即可求出AD2+BC2=AB2+CD2,
(2)把BC=2AD,AB=12,CD=9,代入AD2+BC2=AB2+CD2求解即可得出AD的长,利用周长公式求解即可.
(2)把BC=2AD,AB=12,CD=9,代入AD2+BC2=AB2+CD2求解即可得出AD的长,利用周长公式求解即可.
解答:解:(1)∵AC和BD相交于点O,
∴AO2+DO2=AD2,BC2=BO2+OC2,
∴AD2+BC2=AO2+DO2+BO2+OC2=AO2+BO2+(DO2+OC2)=AB2+CD2;
∴AD2+BC2=AB2+CD2;
(2)∵BC=2AD,AB=12,CD=9,
∴AD2+(2AD)2=122+92,
解得AD=3
.
∴BC=2AD=6
,
∴四边形ABCD的周长=AD+BC+AB+CD=3
+6
+12+9=21+9
.
∴AO2+DO2=AD2,BC2=BO2+OC2,
∴AD2+BC2=AO2+DO2+BO2+OC2=AO2+BO2+(DO2+OC2)=AB2+CD2;
∴AD2+BC2=AB2+CD2;
(2)∵BC=2AD,AB=12,CD=9,
∴AD2+(2AD)2=122+92,
解得AD=3
| 5 |
∴BC=2AD=6
| 5 |
∴四边形ABCD的周长=AD+BC+AB+CD=3
| 5 |
| 5 |
| 5 |
点评:本题主要考查了勾股定理,解题的关键是熟记勾股定理的灵活运用.

练习册系列答案
相关题目
绵阳科技城是四川省第二大城市,2012年国民生产总值约为14000000万元,用科学记数法表示应为( )万元.
| A、14×107 |
| B、1.4×107 |
| C、1.4×106 |
| D、0.14×107 |
若等腰直角三角形的直角边长为2cm,则它的外接圆的面积是( )
| A、2π | B、4π | C、8π | D、16π |
 如图,菱形ABCD的边长为5,对角线AC=6.则菱形ABCD的面积为
如图,菱形ABCD的边长为5,对角线AC=6.则菱形ABCD的面积为

 如图是抛物线拱桥,已知水位在AB位置时,水面宽4
如图是抛物线拱桥,已知水位在AB位置时,水面宽4