题目内容
13．约分：（1）$\frac{15x{y}^{2}}{25{y}^{3}z}$；
（2）$\frac{12x{y}^{2}+9xyz}{3{x}^{2}y}$；
（3）$\frac{{m}^{3}-m}{4m+4}$；
（4）$\frac{9{a}^{2}+24ab+16{b}^{2}}{3a+4b}$．
分析 （1）先找出公因式5x2，然后约分即可；
（2）先找出公因式3xy，然后约分即可；
（3）先把分子分母因式分解，然后约分即可；
（4）先把分子因式分解，然后约分即可．
解答 解：（1）$\frac{15x{y}^{2}}{25{y}^{3}z}$=$\frac{3x}{5yz}$；
（2）$\frac{12x{y}^{2}+9xyz}{3{x}^{2}y}$=$\frac{4y+3z}{x}$；
（3）$\frac{{m}^{3}-m}{4m+4}$=$\frac{m（m+1）（m-1）}{4（m+1）}$=$\frac{{m}^{2}-m}{4}$；
（4）$\frac{9{a}^{2}+24ab+16{b}^{2}}{3a+4b}$=$\frac{（3a+4b）^{2}}{3a+4b}$=3a+4b．
点评 本题考查了约分：约去分式的分子与分母的公因式，不改变分式的值，这样的分式变形叫做分式的约分．
练习册系列答案
相关题目
如图共有9不同的四边形．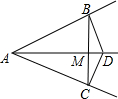
点D是∠BAC的平分线上一点，过点D作DB⊥AB于点B，DC⊥AC于点C，连接BC交AD于点M．求证：
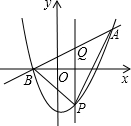如图，二次函数y=$\frac{1}{2}$x2+bx+c的图象与x轴交于B、C两点（点B在点C的左侧），一次函数y=kx+1的图象经过点B和二次函数图象行另一点A．其中点A的坐标为（4，3）．