题目内容
8.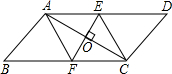 如图,在平行四边形 ABCD中,对角线AC的垂直平分线分别与AD,AC,BC相交于点E、O、F,求证:四边形AFCE是菱形.
如图,在平行四边形 ABCD中,对角线AC的垂直平分线分别与AD,AC,BC相交于点E、O、F,求证:四边形AFCE是菱形.
分析 先根据平行四边形的性质得到OA=OC,AD∥BC,再证明△AOE≌△COF得到OE=OF,根据对角线互相平分的四边形为平行四边形得到四边形AFCE为平行四边形,接着根据线段垂直平分线的性质得EA=EC,然后根据有一组邻边相等的平行四边形是菱形即可得到结论.
解答 解:∵四边形ABCD为平行四边形,
∴OA=OC,AD∥BC,
∴∠EAC=∠ECA,
在△AOE和△COF中
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{OA=OC}\\{∠AOE=∠FOC}\end{array}\right.$,
∴△AOE≌△COF,
∴OE=OF,
∴四边形AFCE为平行四边形,
∵EF垂直平分AC,
∴EA=EC,
∴四边形AFCE是菱形.
点评 本题考查了菱形的判定:一组邻边相等的平行四边形是菱形;四条边都相等的四边形是菱形;对角线互相垂直的平行四边形是菱形.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
19.下列各数:0,-$\sqrt{9}$,1-$\sqrt{2}$,0.2$\stackrel{•}{3}$,$\root{3}{64}$,$\frac{22}{7}$,π,0.303003…,中无理数个数是( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
17.等腰三角形的两边长分别为4和9,这个三角形的周长是( )
| A. | 17 | B. | 22 | C. | 17或22 | D. | 17和22 |
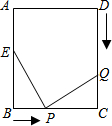 如图,已知长方形ABCD的边长AB=16cm,BC=12cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上由点D向C点运动.则当△BPE与△CQP全等时,P运动时间t为1或3s.
如图,已知长方形ABCD的边长AB=16cm,BC=12cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上由点D向C点运动.则当△BPE与△CQP全等时,P运动时间t为1或3s.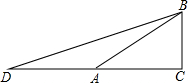 如图所示,在△ABC中,∠C=90°,D是CA延长线上一点,∠BDC=15°,AD=AB=4,则BC=2.
如图所示,在△ABC中,∠C=90°,D是CA延长线上一点,∠BDC=15°,AD=AB=4,则BC=2.